Er is veel discussie over het stelsel van de inkomstenbelasting en de toeslagen, waarbij er vraagtekens worden gezet bij de complexiteit, doelmatigheid en herverdeling binnen het stelsel. Het realiseren van een brede herziening is tot op heden onmogelijk gebleken. In dit artikel worden kansrijke en kansarme wijzigingen in het stelsel geanalyseerd.
In het kort
– De optimale tariefstructuur hangt af van de voorkeuren voor herverdeling, en is niet vlak.
– De marginale druk voor de middengroepen is relatief hoog.
– Een hoger tarief aan de top levert weinig op.
De laatste jaren passeren er diverse voorstellen de revue voor wijzigingen in het stelsel – zoals een vlaktaks, een basisinkomen, een hoger of lager toptarief, ofwel meer of minder ondersteuning van een- en/of tweeverdieners, et cetera (CPB, 2017). Hoe ziet een doelmatige doch rechtvaardige inkomstenbelasting er dan uit? Dit is het domein van de optimale-belastingtheorie (Mirrlees, 1971). De optimale-belastingtheorie gaat over de vraag hoe de optimale tariefstructuur eruit moet zien gegeven de inkomensverdeling, de mate waarin de inkomensverdeling reageert op belastingen, en de maatschappelijk waarde van een extra euro inkomen voor verschillende inkomensgroepen. De optimale tariefstructuur die daaruit volgt kunnen we vergelijken met de bestaande tariefstructuur. Daarmee krijgen we inzicht in kansrijke en kansarme hervormingen van de tariefstructuur, zoals de (on)wenselijkheid van een vlaktaks of een hoger toptarief. Mede dankzij het werk van Diamond (1998) en Saez (2001; 2002) heeft de optimale-belastingtheorie aan belang gewonnen voor de beleidsanalyse, waarbij er gepoogd wordt om zo veel mogelijk op basis van empirische kennis uitspraken te doen over de optimale tariefstructuur.
In deze bijdrage worden de methoden van de optimale-belastingtheorie toegepast voor Nederland. We gaan daarbij op zoek naar de optimale vormgeving van de tariefstructuur in Nederland: hoe hoog moeten de tarieven zijn voor de verschillende inkomensgroepen? Vervolgens wordt er dieper ingegaan op de optimale tariefstructuur voor alleenstaande ouders, een groep die relatief veel aandacht heeft gekregen in de beleidsdiscussie.
De resultaten die hier worden gepresenteerd, zijn gebaseerd op recente modellen van de optimale-belastingtheorie1, en op recent onderzoek naar de gedragsreacties van wijzigingen in de inkomstenbelasting en de toeslagen2, zowel op de extensieve marge (participatie) als de intensieve marge (uren per week), en in termen van zowel gewerkte uren als de belastinggrondslag meer in het algemeen (de zogenaamde ‘elasticiteit’ van het belastbaar inkomen).
Een korte introductie in de optimale-belastingtheorie
Wat is de optimale tariefstructuur bij een gegeven voorkeur voor herverdeling? Mirrlees (1971) wist een antwoord te geven op deze vraag, in een artikel dat hem in 1996 de Nobelprijs voor Economie opleverde. In het kort, werkt zijn model als volgt. Personen verschillen in verdiencapaciteit. Het inkomen van personen wordt bepaald door een combinatie van de verdiencapaciteit (gegeven) en de inspanning die personen verrichten (keuze), waarbij personen met een hogere verdiencapaciteit uiteindelijk ook een hoger inkomen hebben. De overheid wil gaan herverdelen van personen met een hoge verdiencapaciteit naar personen met een lage verdiencapaciteit, omdat een extra euro meer waard is voor degenen met een lage verdiencapaciteit dan voor degenen met met een hoge verdiencapaciteit. De overheid neemt echter alleen het inkomen waar en niet de verdiencapaciteit. De herverdeling van hoge naar lage inkomens belast daarmee niet alleen de verdiencapaciteit, maar ook de inspanning die personen leveren. Dit leidt tot doelmatigheidsverliezen. De overheid gaat dan op zoek naar een second-best oplossing waarbij men de belastingtarieven zo kiest dat de herverdelingswinst aan de marge gelijk is aan de doelmatigheidsverliezen. Mirrlees (1971) loste deze vraag op, maar het antwoord was nog dermate ontoegankelijk en algemeen dat het slechts weinig richting gaf aan beleid. Op basis van een aantal versimpelende aannames presenteerde Diamond (1998) de meer toegankelijke ABC-formule, die de optimale tariefstructuur bepaalt. Deze behandel ik hieronder in meer detail. Saez (2001) heeft dit model vervolgens omgeschreven in zogenaamde sufficient statistics die grotendeels empirisch zijn waar te nemen (met uitzondering van de sociale-welvaartsgewichten) en heeft het empirisch ingevuld voor de VS. Dankzij Diamond (1998) en Saez (2001) geeft de optimale-belastingtheorie nu veel meer richting aan beleid.
Diamond (1998) laat zien dat, onder een aantal versimpelende aannames (zoals de afwezigheid van inkomenseffecten), het optimale marginale belastingtarief t(y) bij een bepaald inkomen y gegeven wordt door de ABC-formule:
t(y) / (1 – t(y)) = A(y)B(y)C(y)
Voor ieder inkomen y wordt daarmee het optimale marginale tarief bepaald, en dus de hele tariefstructuur naar inkomen.3 Een hogere waarde voor A, B of C bij een gegeven inkomen y levert dus een hoger optimaal marginaal tarief op bij dat inkomen. De waarde van de termen A, B en C is als volgt:
A(y) = 1/ε. Hierin is ε de elasticiteit van het belastbaar inkomen naar (1 minus) het marginale belastingtarief. Hoe hoger ε, hoe groter de verstoring door de belasting, hoe kleiner A, en hoe lager dus het optimale marginale tarief bij een gegeven inkomen.
B(y) = 1 – G(y). Hierin is G(y) de gemiddelde maatschappelijke waarde van een extra euro voor iedereen met een inkomen hoger dan y. Daarbij geldt G(0) = 1, de gemiddelde waarde van een extra euro is gelijk is aan 1. Verder nemen we aan dat de G′(y) < 0; de gemiddelde maatschappelijke waarde van een euro daalt naarmate we hoger in de inkomensverdeling komen, omdat het individueel marginaal nut van een extra euro daalt in inkomen, of omdat de maatschappelijke waardering van het individueel marginaal nut van een extra euro daalt in inkomen (Saez, 2001). Omdat G′(y) < 0 geldt B′(y) > 0, de wens om te herverdelen leidt er ceteris paribus toe dat de marginale tarieven stijgen in inkomen.
C(y) = (1 – F(y)) / yf(y). Hierin is de teller 1 – F(y) het aandeel personen met een inkomen boven y. In zekere zin weegt deze term de herverdelingswinst B(y); als er nog veel personen zijn met een inkomen boven y, dan zijn er nog veel personen van wie het inkomen kan worden herverdeeld naar lagere inkomens. De noemer yf(y) is de belastinggrondslag op het inkomen y. In zekere zin weegt deze term het doelmatigheidsverlies A(y), de doelmatigheidsverliezen zijn groter naarmate het inkomen y of het aandeel personen f(y) bij een gegeven inkomen hoger zijn. De term C(y) heeft empirisch grotendeels een U-vorm (met een lagere rechterpoot) in inkomen y. Bij een laag inkomen zitten er nog veel personen met een inkomen boven y: 1 – F(y) is hoog; en de belastinggrondslag die verstoord wordt, is laag: yf(y) is laag. Rond modaal zitten er inmiddels minder personen met een inkomen boven y: 1 – F(y) is lager, maar de belastinggrondslag die wordt verstoord, is hoog: yf(y) is hoog, vooral omdat daar veel personen f(y) zitten. Bij hoge inkomens daalt vervolgens zowel de teller als de noemer, en is het een empirische vraag of C(y) toe- of afneemt. Empirisch blijkt C(y) weer op te lopen, tot uiteindelijk een constante (Jacobs et al., 2013).
De optimale marginale tarieven volgen grotendeels de U-vorm van C(y), die direct volgt uit de inkomensverdeling. Stel dat de elasticiteit van het belastbaar inkomen constant is over de inkomensverdeling. Volgens Jongen en Stoel (2019) is dat geen slechte benadering. Verder geldt dat B(y) oploopt in inkomen. Hoe snel dat gebeurt, hangt af van de voorkeuren voor herverdeling (bij sterke voorkeuren voor herverdeling loopt B(y) sneller op). Dan hebben de optimale marginale tarieven uiteindelijk bij benadering ook de U-vorm van de C(y)-term (Diamond, 1998): hoog aan de onderkant, laag voor de middengroepen, en weer wat hoger aan de bovenkant. Dit is grafisch weergegeven in figuur 1. Deze vorm is robuust voor verschillende politieke voorkeuren aangaande herverdeling (zolang de maatschappelijke waarde van een extra euro maar daalt in inkomen).
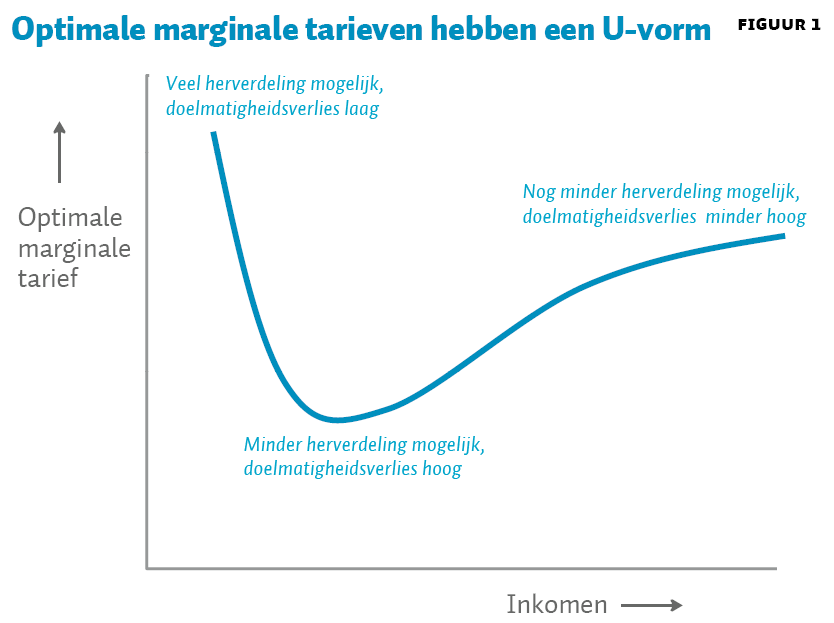
Voordat we overgaan naar de empirische toepassing van Nederland behandelen we kort nog twee varianten van het model van Mirrlees (1971). Ten eerste, het standaardmodel van Mirrlees negeert de extensieve marge in het arbeidsaanbod. Maar belastingen verstoren zowel de extensieve marge (participatie), als de intensieve marge (uren per week of loon- en winstinkomen per werkende). De extensieve marge kan worden gemodelleerd door mensen een keuze te laten maken tussen wel en niet werken, waarbij, om te kunnen werken, mensen de vaste kosten van werk moeten incasseren. Toevoegen van de extensieve marge leidt tot een aangepaste ABC-formule (Jacquet et al., 2013, Jacobs et al., 2017), waarbij de B(y)-term doorgaans wat lager is (hogere marginale tarieven leiden hoger in de inkomensverdeling tot hogere gemiddelde tarieven, dit verlaagt de arbeidsparticipatie waardoor de baten van herverdeling afnemen). In de empirische toepassing gebruiken we de aangepaste ABC-formule met zowel extensieve als intensieve marge. Ten tweede, we kunnen de ABC-formule ook omschrijven zodat de herverdelingsvoorkeuren aan de linkerkant komen te staan. Dit is de zogenaamde ‘omgekeerde optimale-belastingmethode’, voor de inkomstenbelasting als eerste toegepast door Bourguignon en Spadaro (2012). De vraag is dan: gegeven de inkomensverdeling, gegeven hoe de belastinggrondslag reageert op de belastingen, en gegeven dat een bepaald belastingstelsel optimaal is – wat zal dan de impliciete sociale-welvaartsfunctie (= set van sociale-welvaartsgewichten) zijn? In dit geval gaan we op zoek naar de impliciete herverdelende voorkeuren waarbij een bepaald belastingstelsel optimaal is. De vraag is dan of alle inkomens positief gewaardeerd worden in de sociale-welvaartsfunctie, g(y) > 0 voor alle y, en of personen met een hoger inkomen een lager gewicht krijgen, g′(y) < 0. Merk daarbij op dat bij de omgekeerde optimale-belastingmethode alle verklarende variabelen in principe empirisch te bepalen zijn.
Toepassingen voor Nederland
Hieronder gebruiken we de (gemodificeerde, inclusief inkomens- en participatie-effecten) ABC-formule voor een toegepaste optimale-belastinganalyse voor Nederland, inclusief een omgekeerde optimale-belastinganalyse. We beginnen met een analyse van de algemene tariefstructuur en analyseren vervolgens de optimale inkomensondersteuning voor alleenstaande ouders.
Optimale tariefstructuur, model en kalibratie
Allereerst analyseren we de algemene tariefstructuur. Hoe zien de optimale marginale tarieven er in Nederland uit voor de verschillende voorkeuren wat betreft herverdeling, en hoe verhouden die zich tot het huidige stelsel?
Voor de analyse gebruiken we het optimale-belastingmodel van Jacquet et al. (2013) en Jacobs et al. (2017), waarbij personen aan zowel de extensieve marge (participatie) als de intensieve marge (uren of inkomen) kunnen reageren op financiële prikkels. De consumptie is gelijk aan het netto-inkomen van de persoon. We negeren daarbij dat een deel van de personen een partner heeft, en dat zij kunnen sparen of lenen. Voor een uitgebreide bespreking van het model en de kalibratie-methode, zie Jacobs et al. (2017).
Voor de kalibratie maken we gebruik van de inkomensverdeling in 2015 (meer specifiek de inkomensverdeling in 2012, opgehoogd naar 2015) uit het Inkomenspanelonderzoek van het CBS, een representatieve steekproef van ongeveer 100.000 personen. Voor de bovenste tien procent van de inkomensverdeling plakken we hier een Pareto-verdeling aan vast, die een goede fit geeft voor de top van de inkomensverdeling (Jacobs et al., 2013). Het nut van personen wordt bepaald door consumptie (positief) en inspanning (negatief), en door de vaste kosten of baten van het werk (deze treden alleen op als de persoon werkt). De parameters in de nutsfunctie zijn zo gekozen dat de ongecompenseerde elasticiteit van de intensieve marge gemiddeld gelijk is aan 0,2, wat conservatiever is dan de elasticiteitsschatting van het belastbaar inkomen voor werknemers van 0,24 in Jongen en Stoel (2019) en vergelijkbaar met de schatting van 0,20 van de elasticiteit van het belastbaar inkomen voor werknemers in Bosch en De Boer (2019). De gecompenseerde elasticiteit is gemiddeld gelijk aan 0,25, wat een gemiddelde relatief lage inkomenselasticiteit van −0,05 impliceert, in lijn met de empirie (zie bijvoorbeeld Saez et al., 2012). We hebben in de kalibratie gekozen voor de elasticiteit van het belastbaar inkomen als de intensieve-marge-elasticiteit, omdat de elasticiteit van het belastbaar inkomen meer gedragsreacties vangt van de wijzigingen in marginale tarieven dan alleen de gewerkte uren. De verdeling van de vaste kosten en baten van arbeidsparticipatie is zodanig gekozen dat we uitkomen op een gemiddelde extensieve-marge-elasticiteit van 0,2, in lijn met de gemiddelde extensieve-marge-elasticiteit over groepen in MICSIM (Jongen et al., 2015), en dat de participatiegraad spoort met de data. De effectieve marginale tarieven in het belastingstelsel voor 2015 zijn berekend met het MIMOSI-model van het CPB, waarbij er in principe rekening wordt gehouden met alle (landelijke) inkomensafhankelijke tarieven, belastingkortingen en toeslagen.5
Optimale tariefstructuur, uitkomsten
Vullen we vervolgens de (gemodificeerde) ABC-formule in voor Nederland, dan krijgen we de uitkomsten in figuur 2. Ook voor Nederland, en rekening houdend met effecten op de extensieve marge en het inkomen, vinden we dan dat de optimale marginale tarieven een U-vorm hebben. De marginale tarieven moeten relatief hoog zijn voor lage inkomens, een stuk lager voor de middeninkomens, en vervolgens weer wat hoger voor de topinkomens. De precieze waarde hangt daarbij wel af van de voorkeuren voor herverdeling. Dit lijkt een open deur, maar regelmatig wordt gevraagd naar het optimale stelsel, waarop dus geen eenduidig antwoord bestaat.
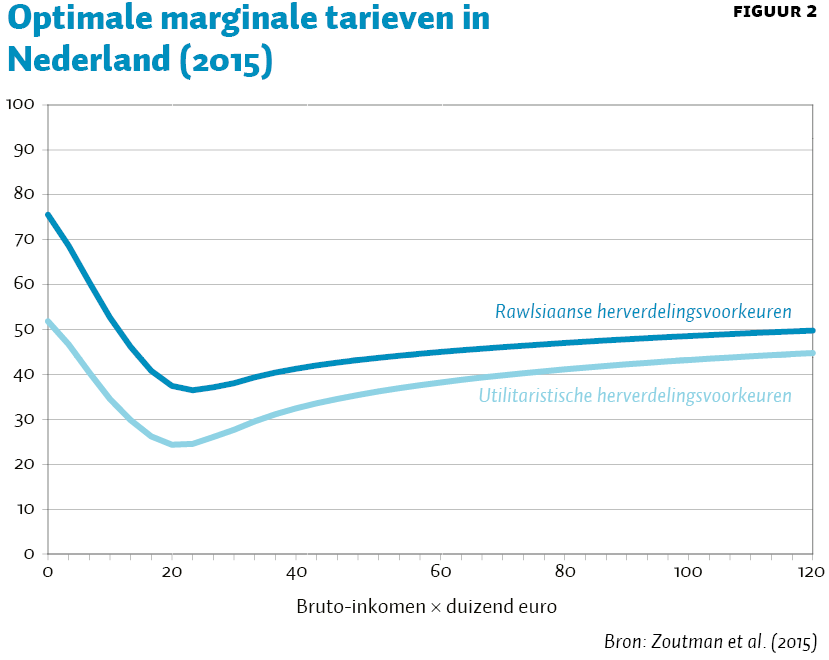
We geven de resultaten voor een zogenaamde rawlsiaanse sociale-welvaartsfunctie, waarbij alleen de persoon met het laagste inkomen een positief gewicht krijgt6, en voor een utilitaristische sociale-welvaartsfunctie, waarbij de maatschappelijke welvaart gelijk is aan de som van de persoonlijke nutten.7 Bij een rawlsiaanse sociale-welvaartsfunctie zijn de marginale tarieven hoger, meer herverdeling, en bij een utilitaristische sociale-welvaartsfunctie treedt er minder herverdeling op en zijn de marginale tarieven lager. Echter, bij geen van deze sociale-welvaartsfuncties zijn de optimale marginale tarieven vlak. Een vlaktaks is dus niet optimaal. Bij een vlaktaks kan er onvoldoende worden herverdeeld naar lage inkomens, en ook leidt een vlaktaks tot onnodige doelmatigheidsverliezen bij de middengroepen, omdat het marginale tarief daar hetzelfde moet zijn als onder- en bovenin de inkomensverdeling (zie Jacobs (2015) voor een verdere discussie van de voor- en nadelen van een vlaktaks).
Figuur 3 geeft de daadwerkelijke effectieve marginale tarieven in 2015. Vergelijken we de daadwerkelijke marginale tarieven met de marginale tarieven uit de optimale-belastinganalyse dan valt een aantal zaken op. Ten eerste zijn de daadwerkelijke marginale tarieven aan de onderkant relatief laag, in tegenstelling tot de marginale tarieven in de optimale-belastinganalyse. Ten tweede zijn de daadwerkelijke marginale tarieven in buurt van het modale inkomen relatief hoog, op de plek waar de optimale-belastinganalyse aangeeft dat ze juist daar relatief laag zouden moeten zijn. Ten derde zien we dat het toptarief zich in de buurt bevindt van het toptarief bij een rawlsiaanse sociale-welvaartsfunctie, waarbij de maximale belastingopbrengst wordt binnengehaald bij de topinkomens.
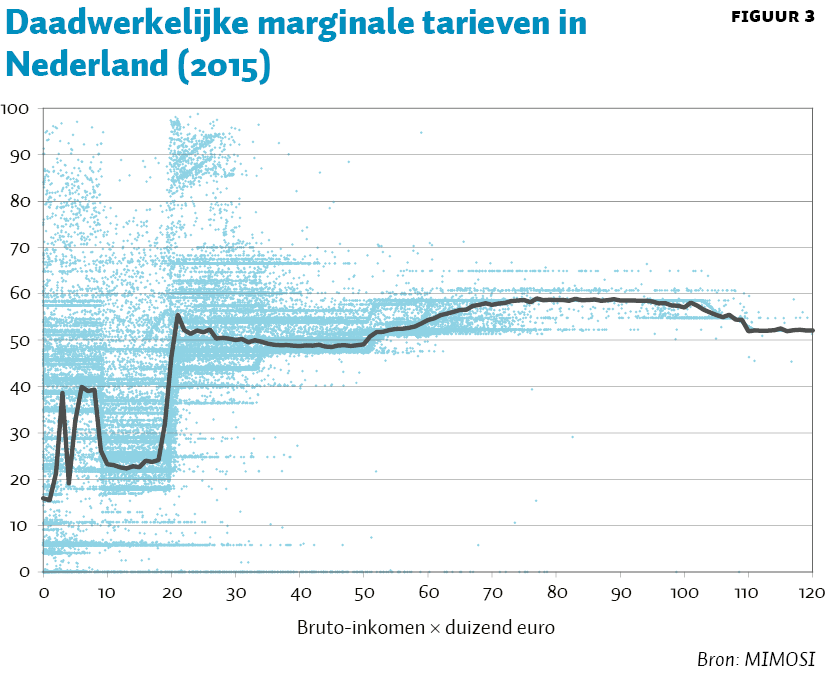
Vanuit de theorie van optimale belastingen is het opmerkelijk dat de marginale tarieven aan de onderkant oplopen, en lokaal een piek hebben nabij de modus van de inkomensverdeling. Figuur 4 laat zien dat dit impliceert dat we aan de lage inkomens een relatief laag sociale-welvaartsgewicht toekennen ten opzichte van de middengroepen – een anomalie (zie Jacobs et al. (2017) voor de methode). Nu bevinden zich onder in de inkomensverdeling relatief veel tweede verdieners, waarvan het persoonlijk inkomen geen goede maatstaf is van hun consumptiemogelijkheden (die door het huishoudinkomen worden bepaald), maar ook als we de analyse doen voor alleenstaanden vinden we een dergelijke inverse U-vorm voor de sociale-welvaartsgewichten (Jacobs et al., 2017). Robuust door de huishoudenstypen heen is dat de marginale druk relatief hoog is voor het meest dichte deel van de inkomensverdeling, de middengroepen. De marginale druk voor de middengroepen is dus volgens de optimale-belastingtheorie te hoog ten opzichte van de marginale druk voor de lage inkomens (en inkomens boven de middengroepen). Jacobs et al. (2017) laten zien dat dit resultaat ook robuust is voor de elasticiteit van de belastinggrondslag: zowel bij een lagere als bij een hogere elasticiteit blijft de ‘anomalie’ voor de middengroepen bestaan. De hoge marginale druk voor de middengroepen heeft onder andere te maken met de afbouw van een aantal inkomensafhankelijke regelingen tussen het minimumloon en modaal (zoals de huurtoeslag). De optimale-belastinganalyse suggereert een snellere afbouw van inkomensafhankelijke regelingen.
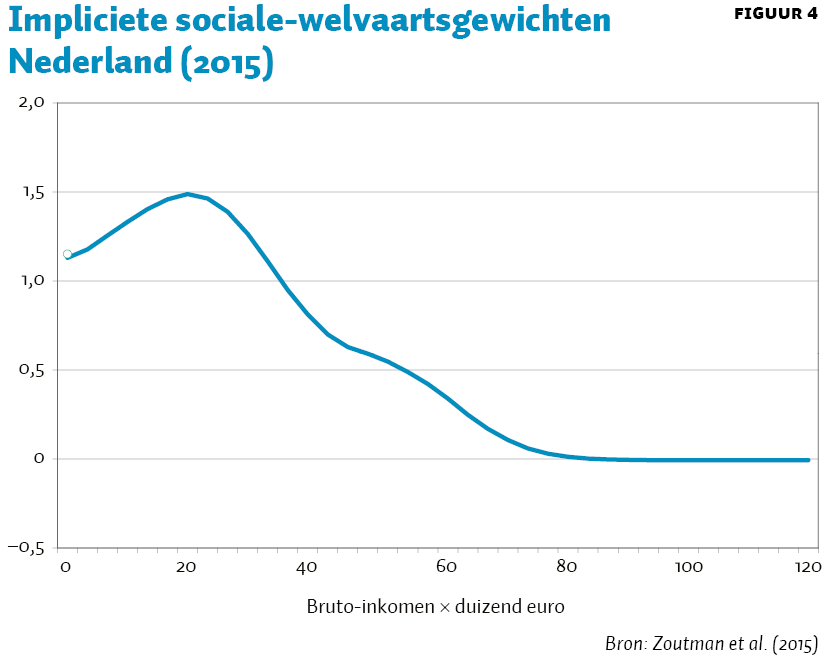
Tot slot analyseren we het toptarief. Figuur 2 en 3 lieten al zien dat het toptarief in 2015 in de buurt lag van het toptarief bij een rawlsiaanse sociale-welvaartsfunctie. Hierbij is de term B(y) aan de top gelijk aan 1, een extra euro aan de top heeft geen maatschappelijke waarde. Dit spoort ook met een sociale-welvaartsgewicht van ongeveer 0 voor de topinkomens in figuur 4. Empirisch blijkt de top van de inkomensverdeling (in Nederland in ieder geval voor de top 10-procent van de inkomensverdeling) op een Pareto-verdeling (Jacobs et al., 2013). Bij een Pareto-verdeling is de term C(y) constant, stel 1/a waarbij a de zogenaamde Pareto-parameter is. Voor Nederland hebben Jacobs et al. (2013) a heel precies geschat op 3,3. De ABC-formule reduceert dan aan de top tot
t(top) / (1 – t(top)) = 1/ε × 1/a -> t(top) = 1 / (1 + εa)
Bij een elasticiteit van het belastbaar inkomen aan de top ε van 0,25 is het opbrengst-maximaliserende toptarief dan ongeveer 55 procent. Dat is vergelijkbaar met een toptarief van 50 procent, nabij het huidige toptarief, en een effectief toptarief van 55 procent (nadat er rekening is gehouden met indirecte belastingen, zie Jacobs et al. (2013)). Dit betekent dat het huidige toptarief in de buurt ligt van de top van de Laffer-curve, en een hoger toptarief weinig tot geen extra belastingopbrengsten oplevert.
Optimale inkomensondersteuning voor alleenstaande ouders
Een beperking van de voorgaande analyse is dat we ervan uitgaan dat voor iedereen hetzelfde belastingstelsel geldt. Dit is echter niet het geval. Alleenstaande ouders krijgen doorgaans een speciale behandeling in het belastingstelsel. In Nederland hebben alleenstaande ouders recht op specifieke inkomensafhankelijke toeslagen en belastingkortingen. Daarbij is de vormgeving een uitdaging, omdat dit een groep is waarbij de maatschappelijke baten van inkomensondersteuning relatief hoog zijn, zij hebben namelijk een relatief laag inkomen en moeten uit dat inkomen ook zorgen voor kinderen, terwijl tegelijkertijd ook de maatschappelijke kosten van inkomensondersteuning relatief hoog zijn. Dus vooral alleenstaande ouders reageren relatief sterk op financiële prikkels, zie Jongen et al. (2015) en Mastrogiacomo et al. (2017). Hieronder analyseren we in hoeverre het beleid erin geslaagd lijkt om een optimale balans te vinden tussen inkomensondersteuning enerzijds, en het behouden van voldoende financiële prikkels voor arbeidsparticipatie anderzijds (zie De Boer en Jongen (2017) voor een meer uitgebreide analyse). We analyseren hier de situatie voor en na de grote hervorming van de inkomensondersteuning voor alleenstaande ouders in 2015, die er mede op gericht was om de financiële prikkels voor arbeidsparticipatie te verbeteren. Een belangrijke kanttekening daarbij is wel dat het een partiële analyse betreft voor alleenstaande ouders, waarbij we alleen uitspraken kunnen doen over de relatieve mate van inkomensondersteuning voor alleenstaande ouders, zoals de werkende versus de niet-werkende alleenstaande ouders. Of de mate van inkomensondersteuning voor de groep alleenstaande ouders als geheel te hoog of te laag is, kunnen we met deze analyse niet vaststellen. Dit hangt in feite mede af van het sociale-welvaartsgewicht dat wordt toegekend aan de groep alleenstaande ouders ten opzichte van de rest.
De hervorming
Voor 2015 was er sprake van een complex stelsel van specifieke inkomensondersteuning voor alleenstaande ouders, zie figuur 5 links. Alle alleenstaande ouders hadden en hebben recht op de kinderbijslag, deze is inkomensonafhankelijk. Daarnaast hadden niet-werkende alleenstaande ouders recht op het inkomensafhankelijke kindgebonden budget (bij een hoger inkomen neemt het kindgebonden budget op een gegeven moment af) en een zogenaamde ‘alleenstaande-ouderkop’ (in de bijstand). Werkende alleenstaande ouders hadden naast de kinderbijslag ook recht op het kindgebonden budget (voor zover hun inkomen niet te hoog was), de alleenstaande-ouderkorting, de aanvullende alleenstaande-ouderkorting en de combinatiekorting.
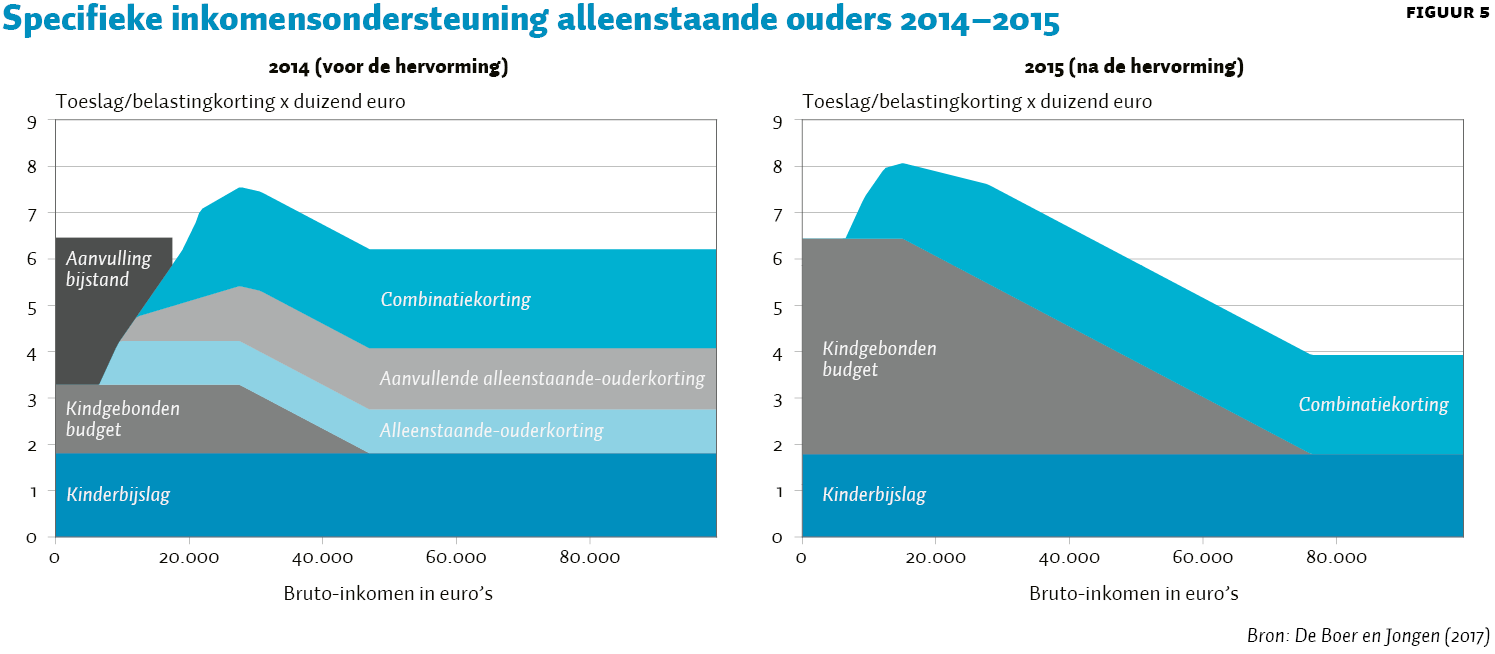
Na 2015 is het stelsel een stuk eenvoudiger geworden, en blijven er nog drie specifieke regelingen over, zie figuur 5 rechts: de kinderbijslag, het kindgebonden budget en de combinatiekorting. Bovendien is de prikkel om te gaan werken voor de meeste alleenstaande ouders verbeterd. Vooral aan de onderkant is die prikkel door de hervorming toegenomen, aan de bovenkant is deze juist afgenomen.
Model en kalibratie
In De Boer en Jongen (2017) wordt de discrete-keuzeversie van de ABC-formule van Saez (2002) gebruikt, zoals geïmplementeerd door Blundell et al. (2009). Alleenstaande ouders kunnen kiezen uit zes discrete inkomenspunten, waarbij optie 0 niet werken is en men in optie 1 tot en met 5 een steeds hoger inkomen heeft. De keuze die alleenstaande ouders maken, hangt af van hun verdiencapaciteit, die verschilt door de groep van alleenstaande ouders heen, en hoeveel deze zich inspannen/werken, waarbij een hoger inkomen een hogere inspanning vereist. De inkomensverdeling over de discrete-keuzepunten is gekalibreerd op de inkomensverdeling van alleenstaande ouders in het Arbeidsmarktpanel van het CBS. De netto-inkomens in de discrete-keuzepunten voor en na de hervorming zijn berekend met MIMOSI van het CPB. De extensieve- en intensieve-marge-elasticiteiten van de belastinggrondslag voor alleenstaande ouders zijn gebaseerd op het MICSIM-model van het CPB. Zie De Boer en Jongen (2017) voor verdere details van het gehanteerde model en de kalibratie.
Uitkomsten voor alleenstaande ouders
Figuur 6 geeft de uitkomsten van de analyse. We presenteren daarbij de impliciete sociale-welvaartsgewichten voor de verschillende discrete-keuzepunten waaruit de alleenstaande ouders in het model kunnen kiezen.8 Optie 0 zijn daarbij de alleenstaande ouders die niet werken, optie 1 bestaat uit alleenstaande ouders met een kleine baan en/of een laag uurloon, en optie 5 zijn de alleenstaande ouders met een grote baan en/of een hoog uurloon.
We zien in figuur 6 dat vóór de hervorming de sociale-welvaartsgewichten weliswaar grosso modo dalen in inkomen en voor alle inkomens positief zijn, consistent met een ‘ordentelijke’ sociale-welvaartsfunctie, maar dat er sprake is van een anomalie voor de werkende alleenstaande ouders met een relatief laag inkomen (discrete-keuze-optie 1). Zij krijgen een lager gewicht dan alleenstaande ouders met een hoger inkomen (discrete-keuze-opties 2 tot en met 4). Na de hervorming in 2015 is deze anomalie verholpen, omdat vooral de inkomensondersteuning voor werkende alleenstaande ouders met een relatief laag inkomen door de hervorming is toegenomen.9
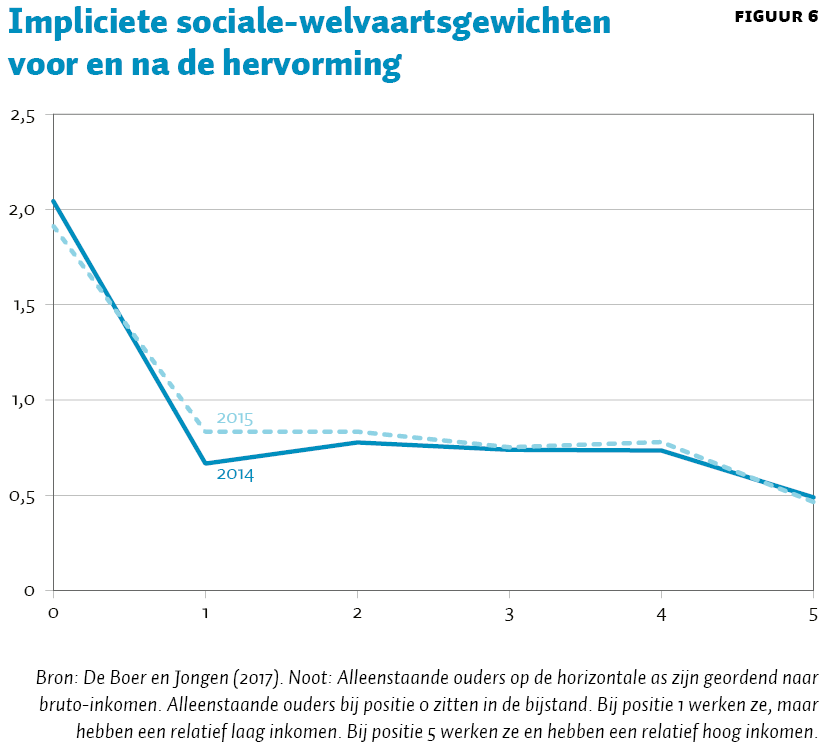
De hervorming van 2015 is dus in ieder geval in twee dimensies succesvol geweest: het stelsel werd een stuk eenvoudiger en een anomalie in de impliciete sociale-welvaartsgewichten is uit het stelsel verdwenen. Is nu het stelsel voor alleenstaande ouders dan optimaal? Daar is helaas geen eenduidig antwoord op, dit hangt onder andere af van de voorkeuren voor herverdeling binnen de groep alleenstaande ouders en tussen de groep alleenstaande ouders en andere groepen in de bevolking. Wat betreft de herverdeling binnen de groep alleenstaande ouders, analyseren De Boer en Jongen (2017) ook de optimale inkomensondersteuning naar inkomen voor alleenstaande ouders bij verschillende voorkeuren voor herverdeling, bij een gegeven totaal budget voor inkomensondersteuning voor alleenstaande ouders. Bij zowel een sterke als een minder sterke voorkeur voor herverdeling wordt gevonden dat de inkomensondersteuning voor alleenstaande ouders met een relatief laag inkomen nog verder kan worden verhoogd, in lijn met de verhoging van de arbeidskorting aan de onderkant sinds 2015. De vraag of de inkomensondersteuning voor niet-werkende alleenstaande ouders, dan wel ouders met een relatief hoog inkomen, omhoog of omlaag moet, is afhankelijk van de voorkeur voor herverdeling.
Tot slot is het nog belangrijk om op te merken dat in dit geval de analyse in De Boer en Jongen (2017) gedaan is nadat de hervorming had plaatsgevonden. Een interessante optie voor toekomstig onderzoek is om een dergelijke analyse vooraf te doen, om dan te kijken in hoeverre een hervorming ons dichter bij een optimaal stelsel brengt of niet, en meer in het algemeen hoe een optimale vormgeving voor bepaalde subgroepen in het belastingstelsel eruit zou kunnen zien (denk daarbij bijvoorbeeld aan de inkomensondersteuning voor alleenstaanden zonder kinderen).
Beperkingen van de analyse
De voorgaande optimale-belastinganalyses voor Nederland geven ons interessante inzichten in kansrijk beleid om de tariefstructuur nog verder te optimaliseren. Tegelijkertijd is het belangrijk om op te merken dat de analyse, hoe geavanceerd soms ook, nog potentieel belangrijke beperkingen kent. Hieronder behandelen we een aantal belangrijke kennislacunes, die tegelijkertijd opties vormen voor toekomstig onderzoek.
We weten nog relatief weinig van wat het verschil verklaart tussen de elasticiteit van het aantal gewerkte uren en de elasticiteit van het belastbaar inkomen (Jongen en Stoel, 2019). Een deel van de verklaring is wellicht dat er in de empirische analyses contractuele uren gebruikt worden, waar de daadwerkelijk gewerkte uren wellicht sterker reageren op wijzigingen in marginale tarieven. Verder spelen belastingontwijking en -ontduiking waarschijnlijk een rol. Daarom is het belangrijk om een decompositie te kunnen maken van de wijzigingen in de belastinggrondslag als gevolg van een wijziging in de marginale tarieven. Voor zover bijvoorbeeld de belastingontwijking leidt tot een toename in een belastinggrondslag elders (of in de toekomst, denk aan pensioenbesparingen), is de elasticiteit van een bepaalde belastinggrondslag niet een sufficient statistic voor de optimale-belastinganalyse (Chetty, 2009, Saez et al., 2012). In dat geval zijn de optimale tarieven doorgaans hoger dan wanneer er geen rekening gehouden wordt met deze zogenaamde fiscale externaliteiten. Een nadere analyse van de elasticiteit van het belastbaar inkomen – inclusief een decompositie naar de onderliggende gedragsreacties, waardoor we beter zicht krijgen op eventuele fiscale externaliteiten – is een interessante optie voor toekomstig onderzoek.
Een andere belangrijke vraag is of personen zich nog wel bewust zijn van wat meer of minder werken financieel oplevert (daarbij wordt het ze ook niet altijd even makkelijk gemaakt door het grote aantal regelingen en de complexiteit daarvan), en op welke toeslagen en kortingen ze recht hebben. Een analyse van de huurtoeslag laat zien dat er sprake is van een aanzienlijk niet-gebruik (Bosch et al., 2019). Dit maakt de huurtoeslag minder effectief als instrument voor herverdeling. Als mensen zich maar beperkt bewust zijn van de financiële prikkels die relevant zijn voor de keuze om al dan niet (meer) te werken, dan kan dit een belangrijke factor zijn in de mate waarin zij reageren op financiële prikkels, zoals bijvoorbeeld inkomensafhankelijke belastingkortingen en toeslagen (zie wederom Bosch et al. (2019) voor een analyse van de gedragseffecten van de huurtoeslag).10 Informatiefricties en andere fricties kunnen ook belangrijke gevolgen hebben voor het bepalen van de langetermijnelasticiteiten van de belastinggrondslag, waarbij lage kortetermijnelasticiteiten consistent kunnen zijn met hoge langetermijnelasticiteiten (Chetty, 2012).
Een beperking van de huidige analyse is verder dat hierbij niet het simultane probleem van de optimale belasting van eerste en tweede verdieners opgelost kan worden. Kleven et al. (2009) laten zien dat dit mogelijk is voor een unitair huishoudensmodel, maar vooralsnog hebben we dat voor Nederland niet weten te implementeren. Zoals in de analyse aangegeven, is een belangrijke ‘verklaring’ voor de relatief lage tarieven aan de onderkant het hoge aandeel tweeverdieners dat een relatief laag inkomen heeft. De ‘anomalie’ dat de tarieven juist relatief hoog zijn voor de middengroepen (ten opzichte van personen met een inkomen daaronder en daarboven), waar de verstoring juist relatief hoog is omdat er veel personen zitten, is echter robuust door de huishoudenstypen heen. Maar meer in het algemeen negeert de analyse dat personen in verschillende huishoudenstypen leven, waarbij bijvoorbeeld schaalvoordelen en de kosten en baten van kinderen een rol spelen. De overheid maakt bij de herverdeling expliciet onderscheid tussen de verschillende huishoudenstypen. De vraag is in hoeverre dat te rationaliseren is vanuit de optimale-belastingtheorie. Dit is een interessante uitdaging voor toekomstig onderzoek (zie Jacobs (2015) voor enkele overwegingen en referenties).
Een andere modelmatige uitdaging is een analyse van optimale belastingen over de levensloop. De inkomensongelijkheid op levensloopbasis is bijvoorbeeld een stuk kleiner dan op jaarbasis (Lever en Waaijers, 2013). Een optimale-belastinganalyse op basis van een realistisch empirisch levensloopmodel voor Nederland is ook een interessante uitdaging voor toekomstig onderzoek. Hetzelfde geldt voor een empirisch onderbouwde optimale-belastinganalyse waarbij expliciet rekening wordt gehouden met preferentie-heterogeniteit, bijvoorbeeld in de voorkeuren voor vrije tijd (Fleurbaey en Maniquet, 2006), wanneer werk op zichzelf (naast inkomen) maatschappelijke waarde heeft (Brett en Jacquet, 2015), of wanneer personen voor zichzelf niet de optimale beslissingen nemen (Gerritsen, 2016). Verder is het belangrijk te beseffen dat bestaande belastingstelsels enerzijds het gevolg zijn van een uitruil tussen doelmatigheid en gelijkheid, en anderzijds van meer strategische politieke overwegingen (Jacobs et al., 2017). De impliciete sociale-welvaartsfunctie zoals we die hebben afgeleid voor Nederland reflecteert dus niet noodzakelijkerwijs de maatschappelijke voorkeuren voor herverdeling.
Conclusies
In deze bijdrage is met behulp van de optimale-belastingtheorie een analyse gemaakt van het huidige stelsel van inkomstenbelasting en toeslagen. Daarbij is gebruikgemaakt van grote representatieve datasets, een geavanceerde bruto-nettocalculator om de effectieve (marginale) belastingdruk te bepalen, recente schattingen van de elasticiteit van participatie, uren en de belastinggrondslag, meer in het algemeen state of the art-simulatiemodellen.
De analyse suggereert het volgende voor de algemene tariefstructuur: er bestaat niet één uniek optimaal belastingstelsel, een optimale tariefstructuur is niet vlak, de marginale druk voor de middengroepen is relatief (te) hoog, en een hoger tarief aan de top levert weinig op. Daarmee lijken de voorstellen voor het invoeren van een vlaktaks (Beetsma et al., 2012), voor het verlagen van de gemiddelde druk voor middengroepen (en daarmee het verhogen van de marginale druk voor middengroepen11) en/of het verhogen van het toptarief (zie de verkiezingsprogramma’s van de ‘linkse’ partijen in CPB (2017)) minder kansrijk wat betreft een efficiënt en rechtvaardig belastingstelsel. Een manier om de marginale druk voor de middengroepen te verlagen is door toeslagen meer te richten op de laagste inkomens, dus door deze sneller af te bouwen. Dit leidt ook tot een afname van het aantal personen dat te maken heeft met toeslagen en daarmee ook van de complexiteit van het belastingstelsel, waarbij tegenwoordig bijna zes op de tien huishoudens een toeslag ontvangen (Bos, 2017). Daarnaast is een analyse behandeld van een subgroep die veel aandacht krijgt in het beleid, namelijk van alleenstaande ouders. Deze analyse suggereert dat het stelsel gericht op alleenstaande ouders inmiddels redelijk is geoptimaliseerd. Bij de analyses zijn er wel de nodige kanttekeningen te maken. Toekomstig onderzoek moet uitwijzen in hoeverre deze kanttekeningen van invloed zijn op de resultaten.
Eindnoten
1 Zie Jacobs et al. (2013), Zoutman et al. (2015), Jacobs et al. (2017), De Boer en Jongen (2017) en De Boer et al. (2018).
2 Zie Bettendorf et al. (2014), Jongen et al. (2015), Bettendorf et al. (2015), Mastrogiacomo et al. (2017), Jongen en Stoel (2019) en Bosch et al. (2019).
3 Meer precies bepaalt Diamond (1998) de ABC-formule voor de (niet-waargenomen) onderliggende vaardighedenverdeling, want de inkomensverdeling is namelijk endogeen. Jacobs et al. (2017) laten zien dat de ABC-formule ook uitgedrukt kan worden met inkomen als argument. In de toepassing wordt een structureel model gebruikt, om rekening te houden met onder andere de endogene inkomensverdeling bij verschillende belastingstelsels, maar dit levert vrijwel identieke resultaten op ten opzichte van een model waarbij sufficient statistics toegepast worden (en genegeerd wordt dat die endogeen zijn), zie Jacobs et al. (2017).
4 Bij het berekenen van de effectieve marginale druk houden we wel rekening met het inkomen van de partner.
5 Deze marginale tarieven worden ook gebruikt om, samen met de intensieve-marge-elasticiteit, de vaardighedenverdeling van werkenden te bepalen uit de inkomensverdeling van werkenden (Jacobs et al., 2017).
6 De marginale tarieven gaan dan niet naar 100 procent omdat je dan niet de maximale hoeveelheid belasting ophaalt, dat is voorbij de top van de Laffer-curve.
7 De marginale tarieven gaan dan niet naar 0 procent omdat er nog steeds sprake is van dalend marginaal nut in inkomen op individueel niveau.
8 Een complicatie daarbij is dat de ‘afstand’ in termen van bruto-inkomen niet gelijk is tussen de verschillende punten; zie De Boer en Jongen (2017) voor de bruto-inkomens die corresponderen met de punten 0 tot en met 5.
9 Een analyse voor subgroepen naar de leeftijd van het jongste kind suggereert dat er, voor alleenstaande ouders met een jongste kind van 0 tot 3 jaar oud, nog steeds sprake is van een anomalie in 2015, waarbij de sociale-welvaartsgewichten van werkende alleenstaande ouders met een relatief laag inkomen lager zijn dan voor werkende alleenstaande ouders met een hoger inkomen. Toekomstig onderzoek moet uitwijzen of de verhoging van de arbeidskorting aan de onderkant na 2015 ook deze anomalie heeft verholpen.
10 De analyse in Jongen et al. (2016) laat zien dat vereenvoudigingen in het stelsel met beperkte koopkrachteffecten wel degelijk mogelijk zijn.
11 Om de gemiddelde druk voor de middengroepen te verlagen moet de marginale druk voor middengroepen omhoog, om meer geld op te halen bij de hogere inkomens en zo de lagere gemiddelde druk voor de middengroepen te financieren.
Literatuur
Beetsma, R., L. Bovenberg, K. Caminada et al. (2012) Elke Nederlander gebaat bij sociale vlaktaks. Artikel op www.mejudice.nl, januari.
Bettendorf, L., K. Folmer en E. Jongen (2014) The dog that did not bark: the EITC for single mothers in the Netherlands. Journal of Public Economics, 119, 49–60.
Bettendorf, L.J., E.L.W. Jongen en P. Muller (2015) Childcare subsidies and labour supply: evidence from a large Dutch reform. Labour Economics, 36, 112–123.
Blundell, R., M. Brewer, P. Haan en A. Shephard (2009) Optimal income taxation of lone mothers: an empirical comparison of the UK and Germany. The Economic Journal, 119(535), F101–F121.
Boer, H.-W. de, en E. Jongen (2017) Optimal income support of lone parents in the Netherlands: are we there yet? CPB Discussion Paper, 361.
Boer, H.-W. de, E. Jongen en P. Koot (2018) Optimal taxation of secondary earners in the Netherlands: has equity lost ground? CPB Discussion Paper, 375.
Bos, W. (2017) Toeslag voor bijna zes op de tien huishoudens. ESB, 101(4743), 344.
Bosch, N. en H.-W. de Boer (2019) Income and occupational choice responses of the self-employed to tax rate changes: heterogeneity across reforms and income. Labour Economics, 58, 1–20.
Bosch, N., E. Jongen, W. Leenders en J. Möhlmann (2019) Non-bunching at kinks and notches of in cash transfers in the Netherlands. International Tax and Public Finance, te verschijnen.
Bourguignon, F. en A. Spadaro (2012) Tax-benefit revealed social preferences. Journal of Economic Inequality, 10(1), 75–108.
Brett, C. en L. Jacquet (2015) Workforce or workfare? The optimal use of work requirements when labour is supplied along the extensive margin. Canadian Journal of Economics, 48(5), 1855–1882.
Chetty, R. (2009) Is the taxable income elasticity sufficient to calculate deadweight loss? The implications of evasion and avoidance. American Economic Journal: Economic Policy, 1(2), 31–52.
Chetty, R. (2012) Bounds on elasticities with optimization frictions: a synthesis of micro and macro evidence on labor supply. Econometrica, 80(3), 969–1018.
CPB (2017) Keuzes in Kaart 2018–2021: een analyse van elf verkiezingsprogramma’s. CPB.
Diamond, P.A. (1998) Optimal income taxation: an example with a U-shaped pattern of optimal marginal tax rates. The American Economic Review, 88(1), 83–95.
Fleurbaey, M. en F. Maniquet (2006) Fair income tax. The Review of Economic Studies, 73(1), 55–83.
Gerritsen, A. (2016) Optimal taxation when people do not maximize well-being. Journal of Public Economics, 144, 122–139.
Jacobs, B. (2015) De prijs van gelijkheid. Amsterdam: Bert Bakker-Prometheus.
Jacobs, B., E. Jongen en F. Zoutman (2013) Over de top. CPB Policy Brief 2013/04.
Jacobs, B., E.L.W. Jongen en F.T. Zoutman (2017) Revealed social preferences of Dutch political parties. Journal of Public Economics, 156, 81–100.
Jacquet, L., E. Lehmann en B. Van der Linden (2013) Optimal redistributive taxation with both extensive and intensive responses. Journal of Economic Theory, 148(5), 1770–1805.
Jongen, E. en M. Stoel (2019) The elasticity of taxable labour income in the Netherlands. De Economist, te verschijnen.
Jongen, E., H.-W. de Boer en P. Dekker (2015) De effectiviteit van fiscaal participatiebeleid. CPB Policy Brief, 2015/02.
Jongen, E., P. Koot en M. Vlekke (2016) Leuker kunnen we het niet maken, wel makkelijker. ESB, 101(4741), 604–607.
Kleven, H.J., C. Thustrup Kreiner en E. Saez (2009) The optimal income taxation of couples. Econometrica, 77(2), 537–560.
Lever, M. en R. Waaijers (2013) Inkomensongelijkheid gedurende de levensloop. TPEdigitaal, 7(1), 140–159.
Mastrogiacomo, M., N. Bosch, M.D.A.C. Gielen en E.L.W. Jongen (2017) Heterogeneity in labour supply responses: evidence from a major tax reform. Oxford Bulletin of Economics and Statistics, 79(5), 769–796.
Mirrlees, J.A. (1971) An exploration in the theory of optimum income taxation. The Review of Economic Studies, 38(2), 175–208.
Saez, E. (2001) Using elasticities to derive optimal income tax rates. The Review of Economic Studies, 68(1), 205–229.
Saez, E. (2002) Optimal income transfer programs: intensive versus extensive labor supply responses. The Quarterly Journal of Economics, 117(3), 1039–1073.
Saez, E., J. Slemrod en S.H. Giertz (2012) The elasticity of taxable income with respect to marginal tax rates: a critical review. Journal of Economic Literature, 50(1), 3–50.
Zoutman, F.T., B. Jacobs en E.L.W. Jongen (2015) Optimal redistributive taxes and redistributive preferences in the Netherlands. Erasmus School of Economics/CPB.
Auteur
Categorieën