De dekkingsgraadsystematiek beschouwt pensioenaanspraken als gegarandeerde nominale uitkeringen, maar pensioenen kennen ook een indexatieambitie en een risico op korting. De huidige systematiek kan die niet op een objectieve manier meenemen. Derivatentheorie kan dit wel en biedt een werkbaar alternatief.
In het kort
– Het pensioen is te beschouwen als een zeer complex derivaat. Vervanging door een eenvoudiger derivaat is aantrekkelijk.
– Met derivatentheorie kan de dekkingsgraadsystematiek worden losgelaten zonder subjectieve verwachtingen te introduceren.
– Voor lange looptijden kan een onzekere geïndexeerde uitkering goedkoper zijn dan een gegarandeerde nominale uitkering.
De Pensioenwet schrijft voor dat pensioenverplichtingen moeten worden gewaardeerd tegen de risicovrije rente. Dat dit zo in de wet staat, is recent nog eens benadrukt door DNB (2018) en door de commissie-Dijsselbloem (2019). Daartegenover hebben verschillende deelnemers aan het pensioendebat betoogd dat waardering met gebruikmaking van het verwachte beleggingsrendement meer voor de hand zou liggen, aangezien fondsdeelnemers risico dragen (Mensonides, 2017; Vlaar, 2019).
De waardering tegen de risicovrije rente zoals vastgelegd in de Pensioenwet is ongetwijfeld mede ingegeven door de wens van de wetgever om te komen tot een objectieve, niet-manipuleerbare maatstaf – een doelstelling die mogelijk op de tocht komt te staan zodra er gerekend wordt met verwacht rendement – maar weerspiegelt niet de intentie van het tweedepijlerpensioen van een welvaartsvast pensioen en ook niet het risico op korten. Door gebruik te maken van een derivaatmodel uit de financiële wiskunde is het echter wel degelijk mogelijk om tot een objectieve waardering te komen van pensioenuitkeringen met een gegeven vorm van onzekerheid. Ik werk zo’n model hier eerst uit alvorens ik inga op de wenselijkheid van het specifieke contract dat in het model wordt gebruikt.
Het pensioencontract als derivaat
Van Wijnbergen (2018) merkt op dat de pensioendeelnemer in het collectieve stelsel in feite een complex derivaat in handen heeft. Hij vergelijkt het pensioenproduct met een zogeheten futures contract, maar Frijns en Mensonides (2018) vinden dat te kort door de bocht. Inderdaad is de complexiteit van het pensioencontract vele malen hoger dan die van enig contract dat op de financiële markten wordt verhandeld. De uitkering die een beginnend pensioendeelnemer uiteindelijk zal krijgen is, via de dekkingsgraad en het beleggingsbeleid van het fonds, afhankelijk van zowel de ontwikkeling van de aandelenrendementen als de geschiedenis van de rentetermijnstructuur over een periode van tientallen jaren – verwerkt onder toepassing van een rijkdom aan uitsmeermethodes en kalibratieregels, die zelf weer onderhevig zijn aan frequente wijzigingen, al naar gelang de uitkomsten van onderhandelingen tussen stakeholders, onder wisselende economische en politieke omstandigheden. Een realistische modellering van dit alles lijkt een hopeloze opgave.
In dit artikel vervang ik daarom dit ultra-complexe derivaat door een eenvoudiger derivaatcontract. In het eenvoudigere derivaatcontract ontvangt de pensioendeelnemer met een bepaalde mate van zekerheid een volledig geïndexeerde uitkering en is er een kleine kans op afstempelen. Bedenk: het liefst ontvangt de deelnemer een volledig geïndexeerde uitkering, maar omdat een honderd procent garantie excessief duur is, accepteert hij een bepaald risico. De vormgeving van dit risico bepaalt het karakter van het pensioenproduct als derivaat. Ter verdere vereenvoudiging bekijk ik daarnaast in deze uitleg een uitkering die plaatsvindt op één moment in de tijd.
We kiezen als ‘onderliggend’ voor het derivaat een breed samengestelde beleggingsindex. De waarde van de index op het tijdstip van inleg wordt als uitgangspunt genomen. Als de index op het tijdstip van uitbetaling in voldoende mate hoger staat, dan volgt een uitkering die volledig voor inflatie is geïndexeerd. Wordt dit niveau niet gehaald, dan vindt een proportionele reductie plaats, tot het peil van een niet-geïndexeerde (nominale) uitkering. Als de beleggingsindex extreem laag staat, dan volgt nog een verdere reductie (afstempelen).
De te kiezen parameters zijn de indexatiezekerheid en de afstempelkans. Een voorbeeld van de uitbetalingsfunctie van het derivaat is weergegeven in figuur 1. Hierbij staat op de horizontale as het gemiddelde indexrendement op jaarbasis gedurende de looptijd. Als het gemiddelde indexrendement hoger is, staat de beleggingsindex dus ook hoger. Als voorbeeld is voor beperkte onzekerheid gekozen in het uitbetalingsprofiel met tachtig procent indexatiezekerheid en twee procent afstempelkans. Ik ga ervan uit dat dit een redelijke balans oplevert tussen onzekerheid enerzijds en kosten anderzijds.
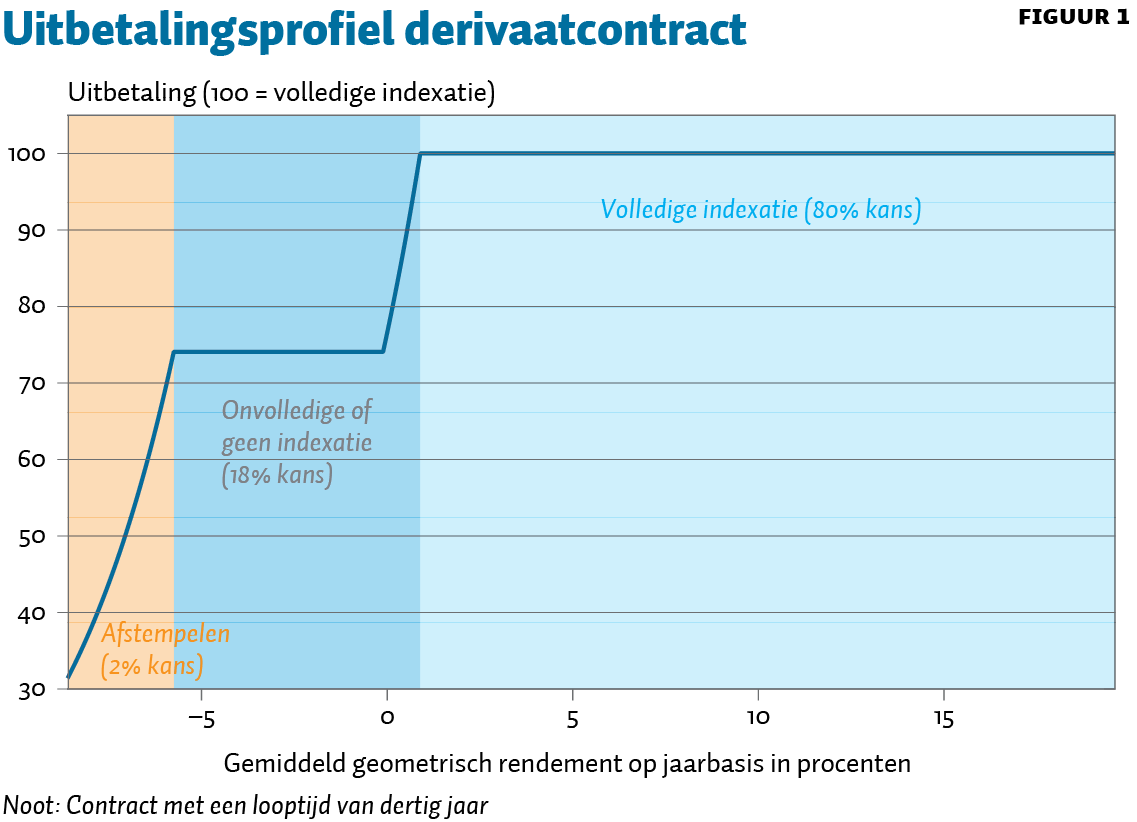
De prijs van het onzekere geïndexeerde contract wordt vervolgens vergeleken met de prijs van het gegarandeerde nominale contract en uitgedrukt in een renteopslag. In vergelijking met de nominale rente, die in de Pensioenwet als uitgangspunt wordt genomen, is er zowel sprake van een afslag (vanwege inflatie) als van een opslag (vanwege onzekerheid). Als de prijs van het onzekere geïndexeerde contract lager is dan van het gegarandeerde nominale contract is de renteopslag positief. Is het andersom, dan is er sprake van een afslag.
Berekening van de prijs en van de opslag
Het derivaat in figuur 1 wordt gewaardeerd met het standaardmodel van de financiële wiskunde, het Black-Scholes-model (zie ook Schumacher (2019) voor soortgelijke exercities). Daarbij gelden de volgende twee veronderstellingen: ten eerste, de beleggingsindex valt samen met de zogeheten benchmark portfolio, ook wel growth optimal portfolio genoemd (Merton, 1971; Platen en Heath, 2006); ten tweede: rente, inflatie en de prijs van risico zijn respectievelijk twee, een en dertig procent. Een prijs van risico van dertig procent betekent dat elke procentpunt extra volatiliteit in risicodragende beleggingen gepaard gaat met 0,3 procentpunt extra verwacht rendement. Dit is consistent met een historisch gemiddelde volatiliteit van aandelen van vijftien procent en een gemiddeld rendement dat 4,5 procentpunt hoger is dan de risicovrije rente.
Met deze veronderstellingen is de inkoopprijs van het onzekere geïndexeerde contract dat over dertig jaar honderd euro geïndexeerd uitbetaald iets minder dan vijftig euro. Merk op: bij een rente van nul procent gaat die prijs naar negentig euro. Pensioendeelnemers zullen dan wellicht meer onzekerheid willen accepteren om de kosten terug te brengen. Figuur 2 toont de netto-opslag als functie van de looptijd voor verschillende waarden van de inflatie bij dezelfde parameterwaarden als bij figuur 1. Als de netto-opslag positief is, dan betekent dit dat bij de gegeven looptijd (uitgezet op de horizontale as) een onzekere geïndexeerde uitkering goedkoper is dan een gegarandeerde nominale uitkering. De vergelijking hangt van het niveau van de inflatie af, maar niet van de rente; als de rente lager is, worden beide producten duurder, maar de onderlinge verhouding blijft gelijk.
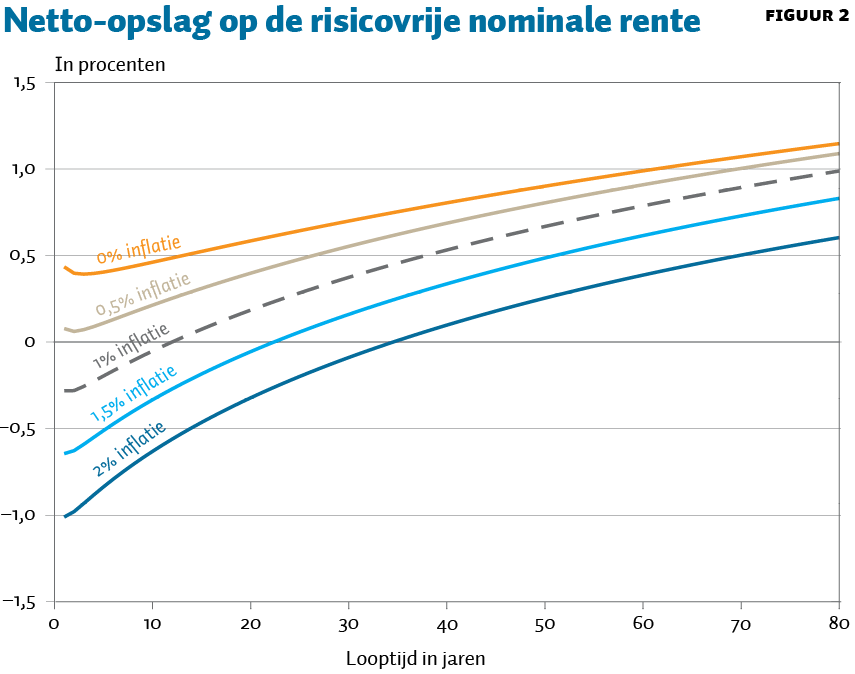
Bij een inflatie van twee procent zou er voor een gegarandeerd volledig geïndexeerde uitkering een afslag op de rente moeten gelden van eveneens twee procent. Figuur 2 toont dat deze afslag wordt beperkt door het accepteren van onzekerheid, en dat er bij voldoende lange looptijden zelfs sprake is van een positieve netto-opslag. Bij lagere inflatie is de afslag minder, maar het effect van de onzekerheid vermindert eveneens, vanwege de (niet volledig harde) nominale garantie. In alle gevallen neemt de netto-opslag toe als de looptijd langer is; dit kan gezien worden als een argument voor ‘vooruitbeleggen’. Het niveau van de netto-opslag wordt hoger bij een lagere indexatiezekerheid en/of een hogere afstempelkans.

Advies uit derivaatmodel
Verdisconteren tegen de nominale rente lijkt zo gek nog niet. Immers, figuur 2 laat zien dat de netto-opslag met betrekking tot de nominale rente afhankelijk van de looptijd zowel positief als negatief kan zijn; gewogen over alle generaties zou het totale effect voor een gegeven fonds op nul kunnen uitkomen. Maar de figuur suggereert ook dat een nauwkeurige berekening uitkomsten genereert die afhangen van de inflatie, en die zullen variëren tussen grijze en groene fondsen.
De opslagen uit figuur 2 geven een beeld van de besparingen die bereikt kunnen worden door het accepteren van een beperkte mate van onzekerheid. Bij een inflatie van één procent en een rente van twee procent is de inleg 74 euro voor een gegarandeerde uitkering van honderd euro over dertig jaar. Bij een indexatiezekerheid van tachtig procent en een afstempelkans van twee procent wordt dit bedrag teruggebracht tot 49 euro.
Figuur 1 laat zien dat afstempelen alleen zal plaatsvinden in scenario’s waarin de beleggingsindex zich dramatisch gedraagt: het gemiddelde jaarlijkse rendement over dertig jaar zou lager moeten uitkomen dan minus 4,75 procent. In zo’n scenario heeft de wereld zoals wij die kennen opgehouden te bestaan en zullen ontvangers van uitkeringen zich waarschijnlijk gemakkelijker neerleggen bij een reductie dan in een situatie waarin er sprake is van een bloeiende economie met stijgende lonen.
Kader 1 – De dekkingsgraadparadox
In het bestaande stelsel wordt de waarde van de verplichtingen niet berekend om een verkoopprijs vast te stellen, maar om beslissingen te nemen, onder meer met betrekking tot de indexatie. De waardering is dus niet een doel op zich, maar dient ter bepaling van een van de ingangsvariabelen in een stuursysteem dat diverse doeleinden heeft, zoals eerlijke verdeling van middelen, niet al te volatiele uitkeringen en vermijding van ongewenste macro-economische effecten.
Dat voor de wettelijke waardering van de verplichtingen een methode wordt gebruikt die berust op veronderstellingen (gegarandeerde nominale aanspraken) die niet met de werkelijkheid corresponderen, is dus op zich geen grond voor kritiek. Het zou in principe kunnen dat juist deze methode leidt tot een uitgebalanceerde sturing waarin de verschillende doelstellingen van het systeem ieder zo goed mogelijk worden gerealiseerd. Dit lijkt echter niet waarschijnlijk, gezien de behoefte die alom wordt gevoeld om aan het systeem te sleutelen.
Natuurlijk zijn er alternatieven. Een vaste rekenrente zou leiden tot een ander stuursysteem waaronder sommige doelen misschien in hogere mate, andere misschien in mindere mate worden bereikt. Hetzelfde geldt voor een systeem met opslagen die ontleend zouden kunnen zijn aan derivaatberekeningen. Maar geen van de rekenmethodes is correct vanuit een oogpunt van waardering: de pensioenaanspraak is niet een gegarandeerde nominale aanspraak, de marktrente is niet vast, de uitbetalingsfunctie die hierboven is verondersteld, klopt niet met het feitelijk uitkeringsbeleid.
Interessant is in dit verband de poging die enige jaren geleden door de Europese toezichthouder EIOPA is gedaan om door middel van een ‘holistic balance sheet’ te komen tot een meer precieze marktwaardering van pensioenaanspraken, met inbegrip van het volledige repertoire aan voorwaardelijke kortingsregels. In de discussie hierover is opgemerkt dat, als werkelijk alle afslag- en bijslagopties worden meegenomen, de dekkingsgraad voor een fonds dat geheel wordt gefinancierd vanuit deelnemersbijdragen, altijd op honderd procent zal uitkomen. Immers, de uitkeringsregels moeten zodanig zijn geformuleerd dat het fonds niet meer kan uitgeven dan het ter beschikking heeft – en minder dan dat is ook niet de bedoeling.
Een wijzer die altijd op honderd procent staat, is geen bruikbare beleidsindicator. Dat leidt tot de dekkingsgraadparadox: de dekkingsgraad is alleen geschikt om beleid mee te maken als de gebruikte waarderingsmethode voor de verplichtingen niet volledig correct is (als waarderingsmethode). De holistic balance sheet is inmiddels door EIOPA bij het grofvuil gezet.
Bruikbaarheid derivaatmodel
Deze waardering steunt volledig op marktparameters en hangt niet af van de samenstelling van de beleggingsportefeuille van het pensioenfonds. Dit is een belangrijk verschil met waarderingsmethoden die gebruikmaken van verwacht rendement.
Toegegeven, het Black-Scholes-model is een sterk gestileerde weergave van de werkelijkheid, maar het model maakt het wel mogelijk om iets te zeggen over de invloed van onzekerheid op de waarde van toekomstige uitkeringen, en de invloed hierop van enkele essentiële parameters.
Het aanzienlijke besparende effect van beperkte onzekerheid wordt in het model gegenereerd omdat is aangenomen dat de hoogte van de uitkeringen wordt bepaald door een breed gespreide beleggingsindex die kan fungeren als benchmark-portfolio. Hierdoor is er een maximale opbrengst van de acceptatie van onzekerheid. Wordt dezelfde mate van onzekerheid anders vormgegeven (dat wil zeggen anders over economische scenario’s verdeeld), dan zal de opbrengst lager liggen. Gegeven de complexiteit van de geldende uitkeringsregels is het moeilijk te zeggen hoe dicht het huidige beleid bij de meest efficiënte keuze ligt, maar gevreesd moet worden dat de kloof vrij aanzienlijk is.
Een alternatief
Binnen het kader van een dekkingsgraadsystematiek moet niet gezocht worden naar een waarderingsmethode voor verplichtingen die goed is als waarderingsmethode, maar naar een methode die op een geschikte manier fout is, zie kader 1. Een derivaatmodel zoals hier gepresenteerd, kan, in een ander perspectief, ook worden opgevat als een vervanging van de huidige dekkingsgraadsystematiek, in plaats van als een benadering ervan. Het model beschrijft een stelsel waarbij sturing van de uitkeringen niet via een dekkingsgraad verloopt (op welke wijze dan ook berekend), maar via een beleggingsindex. Het supercomplexe derivaat van het huidig systeem wordt dan vervangen door een veel simpeler derivaat waarvan de waarde makkelijker in te schatten is, zodat verdenkingen van ongewenste subsidies tussen en binnen generaties beter te weerleggen zijn. Belangrijker nog: in een systeem gebaseerd op een beleggingsindex kan de hoogste opbrengst voor een gegeven onzekerheid worden opgezocht, wat veel lastiger is in een stelsel dat wordt gestuurd via een dekkingsgraad. Minister Koolmees (2019) heeft terecht opgemerkt dat elk kapitaalgedekte stelsel onder druk komt te staan bij lage rentestanden. Dat geeft des te meer reden om te zoeken naar hogere efficiëntie.
Overgaan naar een stelsel waarin uitkeringen worden bepaald aan de hand van een beleggingsindex, in plaats van een dekkingsgraad, is een nogal radicale gedachte die ernstig wringt met het bestaande toezichtskader. Maar het idee kan goed passen in het kader van de fundamentele discussie waartoe Peter Gortzak heeft opgeroepen in het recente themanummer van ESB over het pensioenakkoord (Gortzak, 2019) – en die inderdaad zeer gewenst is, gezien de hachelijke situatie waarin ons pensioenstelsel is terechtgekomen.
Literatuur
Commissie-Dijsselbloem (2019) Advies Commissie Parameters. Bijlage bij Kamerstuk 32043, nr. 485, 21 juni. Te vinden op www.rijksoverheid.nl.
DNB (2018) Wetgevingsbrief 2018. Brief aan de minister van Sociale Zaken en Werkgelegenheid, 19 september. Te vinden op www.rijksoverheid.nl.
Frijns, J. en J. Mensonides (2018) Misvattingen creëren. ESB, 103(4765), 429.
Gortzak, P. (2019) Kom eens uit de loopgraven nu de rente zo laag is. ESB, 104(4777), 395.
Koolmees, W. (2019) Kamerbrief vernieuwing pensioenstelsel, 1 februari. Te vinden op www.rijksoverheid.nl.
Mensonides, J. (2017) Waardeer pensioenverplichtingen met een risico-opslag. ESB, 102(4750), 276–278.
Merton, R.C. (1971) Optimum consumption and portfolio rules in a continuous-time model. Journal of Economic Theory, 3(4), 373–413.
Platen, E. en D. Heath (2006) A benchmark approach to quantitative finance. Berlijn: Springer.
Schumacher, J.M. (2019) A practical policy design method for endowment funds and collective pension funds. Tekst te vinden op researchgate.net.
Vlaar, P. (2019) Toch nog maar een keertje de rekenrente. Artikel op www.mejudice, 25 januari.
Wijnbergen, S. van (2018) Misvattingen in het pensioendebat en de voorstellen van de sociale partners. ESB, 103(4765), 426–427.
Auteur
Categorieën
1 reactie
Het behandelen van risicodragende pensioenverplichtingen als een derivaat is precies wat DNB al jaren doet;.
Zie de reactie van DNB op een vraag mijnerzijds inzake het gebruik van het Black-Scholes-Merton model (B-S-M model), hieronder.
Hartelijk dank voor uw reactie over de berekening van de rentetermijnstructuur (RTS) voor pensioenfondsen. Het uitgangspunt van de UFR (ultimate forward rate) /RTS is de risicovrije rente. Black- Scholes is inderdaad een model om opties te prijzen, maar heeft geen relatie met UFR/RTS. WEL IS HET ZO DAT DE RISICOVRIJE RENTE DE BASIS IS VOOR RISICONEUTRAAL WAARDEREN EN BLACK- SCHOLES IS DE FORMULE VOOR DE RISICO NEUTRALE WAARDERING VAN EEN OPTIE.
Met vriendelijke groet,
Sven Bijsterbosch
De Nederlandsche Bank N.V.
Afdeling Communicatie
Ontkennen had geen zin, want minister Koolmees heeft dit in de beantwoording van Kamervragen van Martin van Rooijen openlijk toegegeven.
DNB ziet pensioenverplichtingen als een financieel product die je vrij kunt verhandelen. Dat dit een fundamentele denkfout is, is inmiddels wel bekend. Er bestaat simpelweg geen markt waarop gehandeld wordt in pensioenverplichtingen
In 2015 zijn de resultaten van onderzoek naar het B-S-M model gepubliceerd onder de titel “THE MIDAS FORMULA”. Deze studie is met de onderwijsprijs bekroond door de KNAW.
Ik citeer hier één van de conclusies:
“EEN ANDERE IN ESSENTIE NIET TE BEPALEN PARAMETER IS DE RISICOVRIJE RENTE. In de wetenschappelijke literatuur wordt hier duidelijk minder aandacht aan gegeven dan aan de volatiliteit. De rente heeft misschien wel een kleinere impact op de optieprijs dan de volatiliteit, maar de rente speelt wel mee. Een te hoge rente betekent een te hoge call- en te lage putprijs, een te lage rente betekent een te lage call- en te hoge putprijs. Een hoge rentestand drijft immers de aandelenprijzen op (zie hoofdstuk Aandelen II, de rente is de drift). Het is eigenlijk aan de investeerder om te bepalen welke constante rente hij gebruikt (gebruiken we bijvoorbeeld de rente op een US Treasury bond of de rente bij de bank?).
Feit is, dat de rente niet constant is. Er zijn daarom ook modellen die de rente beschouwen als een stochastisch proces. Voor de volatiliteit zijn er overigens ook stochastische modellen.”
Op Wikipedia kunt u o.a. het volgende lezen:
LTCM EN DE KREDIETCRISIS
Long Term Capital management was een hedgefonds, in 1994 opgericht en dat failliet ging in 1998, ondanks het feit dat verschillende Nobelprijswinnaars – Myron Scholes en Robert C. Merton - aan het roer stonden.
HET MODEL HEEFT VOOR DE NODIGE PROBLEMEN GEZORGD BIJ LTCM (SIC!) EN DE OP BLACK-SCHOLES GEBASEERDE DERIVATEN HEBBEN VOOR DE BIJNA-INEENSTORTING VAN DE BANKEN GEZORGD.
Vreemd, dat DNB zich desondanks inlaat met types als Black, Scholes en Merton, ook al zijn zij (op Black na, want die was inmiddels overleden) Nobelprijswinnaars.
Bijzonder dat DNB iets kan - het bepalen van de risicovrije rente – waarvan uit onderzoek blijkt dat het nu juist NIET kan.
Bijzonder ook, dat de heer Schumacher een pleidooi voert voor de toepassing van juist dit model.