Dit artikel is de bijlage van Erken en Giesbergen (2017) Nederland in recessie als Chinese huizenbubbel barst.
Een intertemporeel prijsmodel voor de Chinese huizenmarkt
We gebruiken voor de Chinese huizenmarkt een huizenprijsmodel dat is geïnspireerd op het model dat Garretsen et al. (1999) gebruikten om de ontwikkeling van Nederlandse huizenprijzen te schatten:
$$\Delta \log{\frac{H_{i,t}}{\pi_t} }=c+\alpha_1 \Delta \log{r_{t-4}}+\alpha_2 \Delta \log{\frac{L_t}{L_{t-4}}}+\alpha_3 \Delta \log{P_{i,t}}$$
$$+\alpha_4 \log{\frac{H_{i,t-1}}{Y_{i,t-1}}}+\alpha_5 \log{\frac{H_{i,t-5}}{Y_{i,t-5}}} +\delta_i+\epsilon_{it}$$
waarin \(H\) staat voor de gemiddelde huizenprijs per vierkante meter (data van China Real Estate Reports (CREIS) en \(\pi\) voor het inflatiepercentage (data van het National Bureau of Statistics (NBS)). Onze afhankelijke variabele meet dus de reële huizenprijzen per vierkante meter. Verder representeert \(r\) de gewogen gemiddelde hypotheekrente (data van PBoC), \(L\) de omvang van de hypotheekportefeuille bij banken in renminbi (data van China Economic and Industry Database (CEIC) en \(P\) de bevolkingsomvang. Omdat we de eerste afgeleide nemen bij \(\alpha_2\), meet deze term de groei waarmee banken hun hypotheekportefeuille veranderen. \(Y\) is het besteedbare inkomen per hoofd (data van CEIC). De termen \(\alpha_4\) and \(\alpha_5\) meten dus de nominale huizenprijzen in verhouding tot het beschikbare inkomen op de korte en middellange termijn. Tot slot staat \(i\) voor stad, \(t\) voor kwartaal, \(\Delta\) voor de jaar-op-jaarmutatie en is \(\delta\) een dummyvariabele per stad om rekening te houden met niet-geobserveerde heterogeniteit.
Het model is geschat voor een panel van tier-1-, tier-2- en tier-3-steden voor de periode 2010Q2–2014Q4. Vervolgens zijn deze modellen gebruikt om te voorspellen hoe de huizenprijzen zich zouden ontwikkelen in de periode 2015Q1–2016Q3. Door deze voorspelling op basis van de fundamentals te spiegelen aan de daadwerkelijke prijsontwikkeling kunnen we identificeren hoe groot de bubbelcomponent in de prijsontwikkeling is. In tabel 1 staan de schattingsresultaten van de drie panelmodellen. De gewogen gemiddelde hypotheekrente (\(\alpha_1\)) heeft in alle drie de modellen een significant negatief effect op de reële huizenprijzen. Dit is intuïtief plausibel: als de rente stijgt, neemt de betaalbaarheid van en de vraag naar woningen af, wat vervolgens zorgt voor een lagere prijsdruk. De groei van de hypotheekportefeuille bij banken (\(\alpha_2\)) als gevolg van een stijgende vraag naar woningen heeft een significant positief effect in de tier-1- en tier-2-steden. In de tier-3-steden is dit effect niet significant, mogelijk omdat banken vooral extra hypotheekleningen verstrekken in de grotere steden waar minder sprake is van leegstand dan in veel tier-3-steden. De bevolkingsgroei (\(\alpha_3\)) heeft in de tier-3-steden een sterk opwaarts effect op de reële prijzen, maar niet in de tier-1- en tier-2-steden. Het lijkt er dus op dat de sterke urbanisatie in China alleen buiten de grote steden zorgt voor extra vraag en prijsdruk, omdat nieuwkomers (zoals rurale migranten) waarschijnlijk niet in staat zijn om dure woningen in deze grote steden te kopen. Tot slot laat de één kwartaal vertraagde huizenprijs-inkomensratio (\(\alpha_4\)) een significant positief effect zien in de tier-1- en tier-2-steden, terwijl dezelfde variabele vijf kwartalen vertraagd (\(\alpha_5\)) een significant negatief effect laat zien. Deze resultaten zijn min of meer vergelijkbaar met Garretsen et al. (1999). Op korte termijn zorgt een stijgende huizenprijs-inkomensratio voor een nog snellere groei van de reële huizenprijzen, omdat mensen anticiperen en speculeren op verdere prijsstijgingen. Als prijzen echter te sterk gaan afwijken van het inkomen, zal dit na verloop van tijd een rem zetten op verdere prijsstijgingen, doordat de betaalbaarheid steeds verder verslechtert. Het speculatieve kortetermijnmechanisme (\(\alpha_4\)) is niet significant in tier-3-steden, waarschijnlijk omdat in veel van deze steden nog steeds sprake is van een aanzienlijke leegstand.
Tabel 1: Schattingsresultaten Chinees huizenprijsmodel
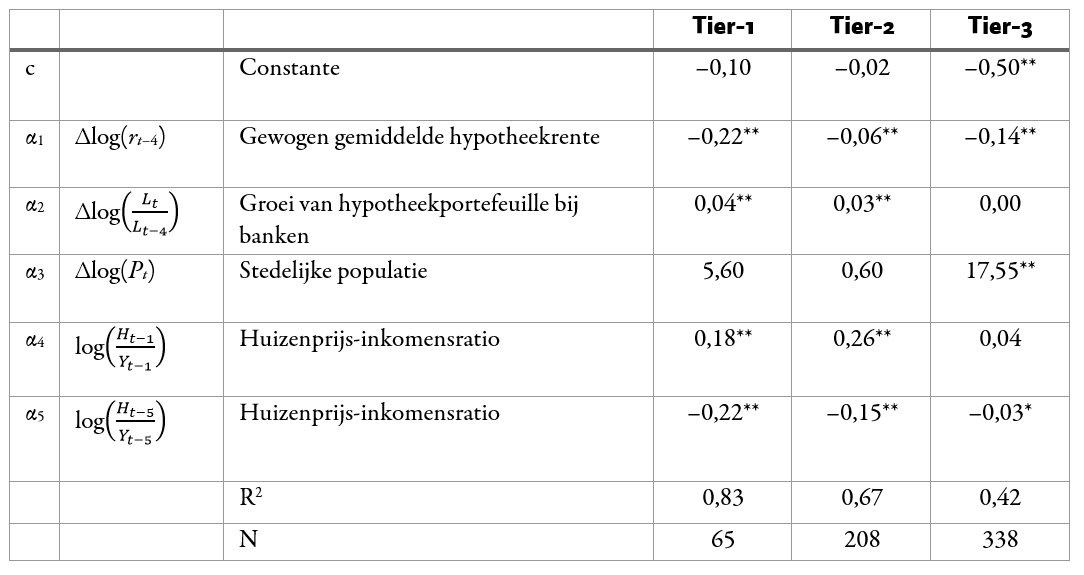
Bron: Rabobank
*/** Significant op respectievelijk tien- en vijfprocentsniveau.
White cross-section standard errors & covariance.
Tabel 2 geeft per kwartaal de procentuele afwijking weer van de huidige woningprijsontwikkeling ten opzichte van de prijs die verwacht wordt op basis de modellen beschreven in tabel 1. Ter illustratie: volgens onze schattingen ligt de huidige vierkantemeterprijs (7.600 euro) van een woning in Shenzhen 25 procent hoger dan wat mag worden verwacht op basis van de onderliggende fundamentals (6.000 euro). Als we de hiervoor genoemde definitie toepassen op de berekeningen voor alle Chinese steden, dan is er sprake van een huizenmarktbubbel in de tier-1-steden Shenzhen en Shanghai, in de tier-2-steden Suzhou, Wuxi, Nanjing, Hefei, Wuhan en Tianjin en in de tier-3-steden Nantong, Wuhu, Dongguan, Zhuhai, Zhengzhou, Tangshan en Shijiazhuang. In sommige tier-3 steden, zoals Wuhu en Zhuhai, is de discrepantie tussen de daadwerkelijke en verwachte woningprijs op basis van ons model zelfs 36 procent. Alle bubbelsteden tezamen tellen 92 miljoen inwoners, wat neerkomt op 12 procent van de totale stedelijke bevolking in China. Dit is een gebied dat qua bevolking even groot is als Duitsland en België bij elkaar en ook nog eens het hart van de economie betreft.
Tabel 2: Bubbelvorming in een selectie van Chinese steden
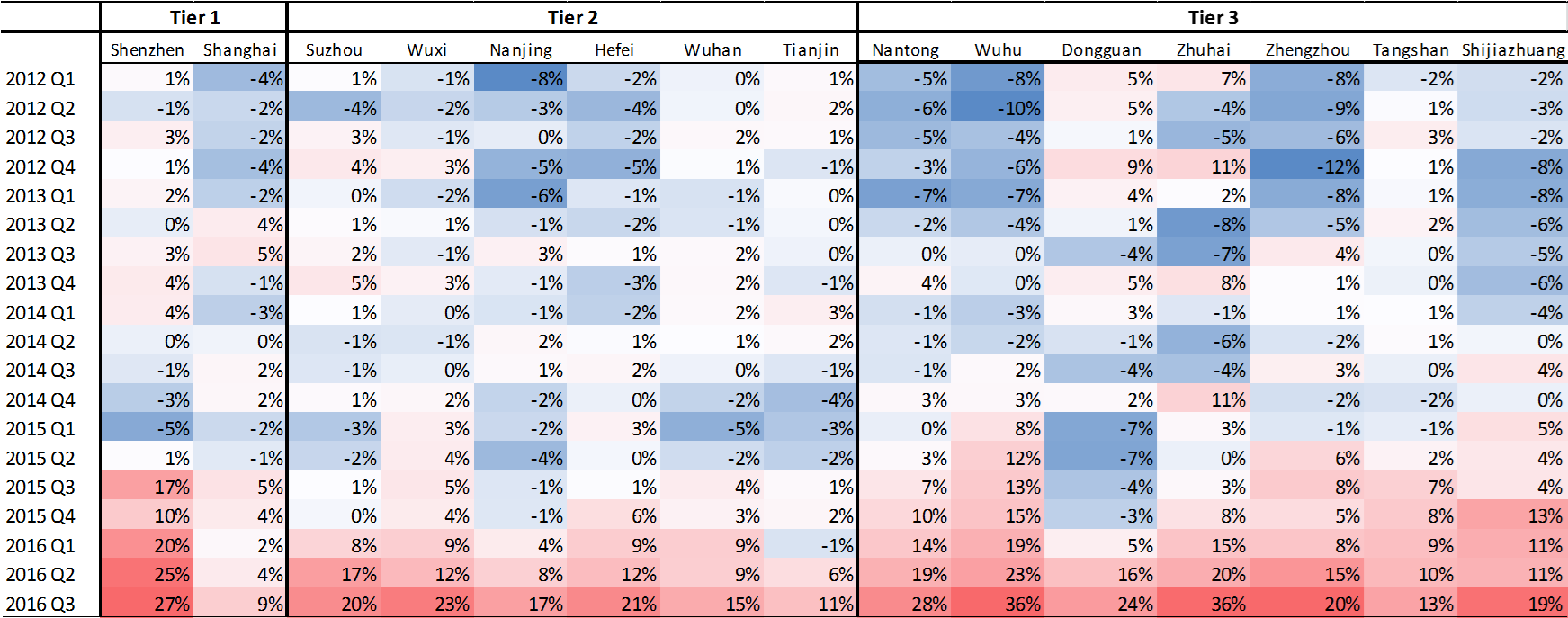
Bron: Rabobank
Auteurs
Categorieën