Dit is een update van mijn blog van 24 december. Aan het einde van deze blog reageer ik op diverse commentaren die ik heb ontvangen en hoe de blog daarop is aangepast. Het betoog en de conclusies zijn onveranderd.
Het afgelopen jaar beweerden talloze collega’s dat iedere begrotingsimpuls in Nederland (vrijwel) volledig weglekt naar het buitenland. Dus is het laten oplopen van het begrotingstekort om de economie te stimuleren zinloos, zo is de redenering. Die veronderstelde ineffectiviteit van begrotingsbeleid vanwege het importlek berust echter op een veel te overdreven inschatting van de weglekeffecten.
Hoe werkt het importlek? Als huishoudens door bezuinigingen en lastenverzwaringen minder inkomen te besteden hebben, kopen ze ook minder geïmporteerde goederen. Nederland kan dus een deel van de koopkrachtdalingen veroorzaakt door bezuinigingen afwentelen op het buitenland.
Als een groot deel van de inkomensdaling weglekt, zou het dus ook geen enkele zin hebben om het begrotingstekort te laten oplopen in een neergaande conjunctuur om zo de economie te stimuleren. De eventuele hogere koopkracht wordt besteed aan buitenlandse in plaats van binnenlandse goederen.
Wie beweren dit? Onder andere collegahoogleraren Sweder van Wijnbergen, Arnout Boot, Roel Beetsma, Pieter Gautier en Jaap Abbring. Maar ook economen als Mattijs Bouman en Marike Stellinga. Ik ben vast nog vele prominente collega’s vergeten hier te noemen.
Sweder van Wijnbergen suggereerde zelfs in het NRC Handelsblad van 9 mei dit jaar dat aan de marge bijna al het inkomen wordt besteed aan buitenlandse goederen: “Meer dan 60 procent van de particuliere consumptie bestaat uit ingevoerde goederen. Dat wordt nog extremer voor de meest conjunctuurgevoelige component van consumptie, duurzame goederen (auto’s, wasmachines et cetera), want die maken wij nauwelijks in Nederland, daar is de invoercomponent dus 100 procent, minus een beetje distributie in de toegevoegde waarde. Dat betekent dat de bestedingsimpuls van onze overheidsuitgaven grotendeels weglekt naar het buitenland.”
Dat laatste is onzin natuurlijk. De belangrijkste conjunctuurgevoelige, duurzame consumptiegoederen zijn huizen. En die worden niet geïmporteerd. Cijfers van het CBS laten zien hoe de consumptie van huishoudens is verdeeld over verschillende uitgavencategorieën. Huishoudens besteden in 2009 iets meer dan 54 procent van hun inkomen aan diensten, waarvan huisvesting met 17,3 procent de belangrijkste is. De meeste van die diensten zijn – net als woningen – niet internationaal verhandelbaar. Denk bijvoorbeeld aan horeca (4,9 procent), medische diensten en welzijnszorg (5,2 procent) of recreatie en cultuur (3,6 procent).
Maar het is waar dat een deel van iedere begrotingsimpuls weglekt naar het buitenland. De Nederlandse invoerquote bedraagt circa 74 procent van het bbp. Dit cijfer en alle volgende cijfers slaan op 2011 en komen uit de nationale rekeningen van het CBS, tenzij anders is vermeld.
Ruim een derde van de invoer bestaat uit wederinvoer. Daarnaast bestaat ongeveer de helft uit invoer van intermediaire goederen, waarvan een groot deel bestemd is voor de export. Beide zijn belangrijk om de effectieve invoerquote te bepalen voor de Nederlandse economie.
Wat is wederuitvoer? Het CBS: “Bij wederuitvoer wordt een Nederlander (tijdelijk) eigenaar van de goederen. Het zijn doorgaans goederen die worden ingevoerd en het land in (vrijwel) onbewerkte staat verlaten. Wederuitvoer wordt opgenomen in de statistieken van de Internationale Handel omdat het eigendomscriterium bepalend is.”
Waarom is die wederuitvoer belangrijk? Als het Nederlandse inkomen daalt, dan heeft dat niet direct effect op de wederuitvoer, omdat die wordt bepaald door de vraag van de Nederlandse handelspartners, voornamelijk in Europa.
Om een vergelijkbare reden is de invoer van intermediaire goederen van belang. Een aanzienlijk deel van die intermediaire goederen wordt gebruikt in de productie van exportgoederen en –diensten. Wederom bepaalt de vraag uit de rest van de wereld via onze exporten hoe groot de invoer is van intermediaire goederen bestemd voor de exporten. Dus de invoerquote moet ook worden geschoond voor invoer van intermediaire goederen bestemd voor de exporten.
Marjolein Jaarsma van het CBS heeft uitgezocht hoe groot het aandeel van de invoer in de exporten is via de wederuitvoer en de invoer van intermediaire goederen. Zij schat dat het importaandeel ruim 55 procent van de totale exporten bedraagt in 2003. Aangezien de uitvoer 83 procent van het bbp bedraagt, is het importaandeel van de export maar liefst 46 procent van het bbp. De effectieve invoerquote bedraagt dus geen 74 procent, maar zo’n 74 – 46 = 28 procent van het bbp, hetgeen nog steeds aanzienlijk is.
Betekent dit dat begrotingsbeleid zinloos is omdat alle begrotingsimpulsen weglekken naar het buitenland? Nee, zelfs in een kleine, open economie als Nederland.
Wat is het effect van het zogenaamde importlek op de effectiviteit van het begrotingsbeleid, dat wil zeggen op de begrotingsmultiplier? Om die vraag te beantwoorden neem ik een huis-tuin-en-keuken IS-LM model voor een kleine open economie (Mundell-Fleming) zoals dat in de meeste eerstejaars macro-economieboeken wordt gebruikt, zie bijvoorbeeld het tekstboek van Mankiw. (Ik heb het iets aangepast, maar de basis blijft hetzelfde.)
Het bbp is Y. Ik neem aan dat de consumptieve bestedingen C afhangen van de rente en het netto besteedbaar inkomen, het bbp minus belastingen, Y – T. De belastingen zijn een constante fractie van het inkomen: T = tY waar t staat voor de (marginale en gemiddelde) belastingdruk. Dus is de consumptie gegeven door: C = C(r,(1 – t)Y). Hoe lager de rente en hoger het besteedbare inkomen, hoe meer de consument gaat uitgeven en lenen (bijvoorbeeld een hypotheek) en hoe minder de consument gaat sparen. Tegelijkertijd neem ik aan dat de bedrijfsinvesteringen I afhangen van de rente (die niet in Nederland wordt bepaald, maar door de ECB) en het bbp Y: I(r,(1 – t)Y). Investeringen gaan omlaag als de rente stijgt, maar stijgen als het besteedbare inkomen hoger wordt. De exporten hangen af van de nominale wisselkoers e en het netto inkomen in het buitenland (1 – t*)Y*: E(e,(1 – t*)Y*). Variabelen in de rest van de wereld worden aangeduid met een asterisk. Hoe hoger het netto inkomen in het buitenland en hoe relatief goedkoper Nederland, hoe meer er wordt geëxporteerd. De importen hangen af van de nominale wisselkoers e en het Nederlandse netto inkomen: M(e,(1 – t)Y). Hoe hoger het inkomen en hoe goedkoper buitenlandse goederen, hoe meer er wordt geïmporteerd.
Merk op dat ik drie afwijkingen heb geïntroduceerd ten opzichte van het model in Mankiw’s tekstboek:
- Importen en exporten hangen af van het netto inkomen en niet het bruto inkomen. Het is eigenlijk heel raar dat dit laatste standaard in macro-modellen wordt opgenomen, want je kunt alleen je netto inkomen uitgeven aan geïmporteerde goederen.
- Consumptie hangt ook af van de rente. Dit is een standaardeigenschap van consumptiefuncties die op basis van intertemporele optimalisatieprincipes worden afgeleid. Maar aangezien de rente toch vaststaat, zie hieronder, maakt het toevoegen van de rente niet uit.
- Investeringen hangen mogelijk ook af van het netto bbp, naast de rente, doordat liquiditeits- en solvabiliteitsposities van bedrijven zijn aangetast en ze moeilijk financiering kunnen krijgen op de kapitaalmarkten om nieuwe investeringen te doen. Bovendien zullen bedrijven meer investeren als ze meer willen produceren. Ik heb daarnaast aangenomen dat bedrijven meer investeren door lagere belastingen. Lagere belastingen op arbeid verlagen de loonkosten en lagere belastingen op winsten maken investeringen rendabeler.
Ik neem aan dat er vaste prijzen zijn (aanname korte termijn) en vaste wisselkoersen e – zoals in het eurogebied – en dat de rentestanden r constant blijven bij een begrotingsimpuls. De rentes staan sowieso dicht bij nul (liquiditeitsval) en de kans dat de ECB de rente gaat verhogen in de huidige, beroerde economische situatie is zo ongeveer nul.
Evenwicht op de goederenmarkt – en daarmee het bbp – volgt uit het ‘Keynesiaanse kruis’:
Y = C(r,(1 – t)Y) + I(r,(1 – t)Y) + G + E(e,(1 – t*)Y*) – M(e,(1 – t)Y).
Aangezien rentes en wisselkoersen constant blijven, zijn de bestedingsmultiplier, de belastingmultiplier en de budget-neutrale multiplier aldus gelijk aan:
ΔY/ΔG = 1/[1 – (1 – t)(c + i – m)],
ΔY/ΔT = – (1 – t)(c + i – m)/[1 – (1 – t)(c + i – m)],
ΔY/ΔG|ΔG=ΔT = 1.
Hier staat c = ∂C/∂(Y – T) > 0 voor de marginale consumptiequote, m = ∂M/∂(Y – T) > 0 voor de marginale importquote, i = ∂I/∂(Y – T) > 0 voor de marginale investeringsquote en t =∂T/∂Y > 0 voor de marginale belastingquote.
Een begrotingsimpuls (uitgavenverhoging, belastingverlaging) kan dus op drie manieren weglekken:
i) via de besparingen (via consumptiequote c), omdat mensen een deel van hun hogere inkomen sparen,
ii) via de belastingen (via belastingquote t) aangezien een deel van het hogere inkomen terugvloeit in de staatskas,
iii) via de importen (via importquote m) omdat een deel van het inkomen in het buitenland wordt besteed.
We kunnen de bovenstaande formules invullen. De marginale consumptiequote uit het besteedbare inkomen is volgens recente schattingen van het CPB zo’n 85 procent. Het aandeel van de belastingen in het bbp bedraagt zo’n 38 procent van het bbp (CBS). We nemen in de berekeningen een marginale belastingquote van 45 procent aan aangezien het marginale tarief veelal boven het gemiddelde tarief ligt wegens de aftrekposten en belastingkortingen.
De ongecorrigeerde, gemiddelde invoerquote is 74 procent van het bbp. De voor de export gecorrigeerde invoerquote is 28 procent van het bbp. Deze geobserveerde invoerquoten worden door (1 – t) gedeeld om m in het model te krijgen.[1] Daarnaast is hierbij de aanname gemaakt dat de gemiddelde invoerquote gelijk is aan de marginale invoerquote. Dat is geen onredelijke benadering. Uit CPB schattingen van de invoervergelijkingen blijkt dat de invoerelasticiteiten rond de 1 liggen (ruwweg constante invoerquotes). Dat impliceert dat het gemiddelde effect ongeveer gelijk is aan het marginale effect, want de elasticiteit geeft de verhouding tussen de marginale verandering ten opzichte van het gemiddelde.
De marginale investeringsquote is in de basisberekeningen op nul gezet, conform het standaard tekstboekmodel. Ik heb ook varianten berekend met een investeringsquote van 0,10 of 0,20. 0,18 is de huidige investeringsquote in het bbp. Het CPB raamt in de investeringsvergelijking van het Saffiermodel een coëfficiënt van 0,4.[2] Net als bij de invoerquote moet de geobserveerde invoerquote gedeeld worden door (1 – t). Ik heb een aantal varianten voor de multipliers berekend met andere waarden van de quoten. De tabel geeft de multipliers volgens bovenstaande formules.
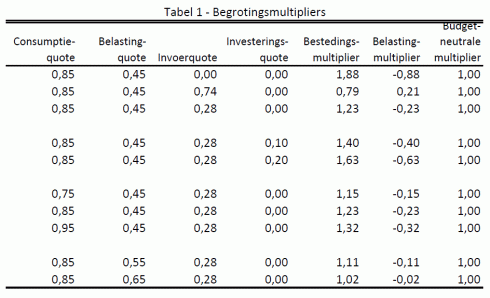
Stel nu dat Nederland een gesloten economie zou zijn (invoerquote m nul) en de investeringen helemaal niet reageren op het bbp (marginale investeringsquote i nul). Wat is dan de bestedingsmultiplier? Antwoord: 1,88. Dat wil zeggen dat als de overheid met 1% bbp bezuinigt, het bbp met 1,88% bbp daalt. Dat is fors.
Wat gebeurt er in de open economie? Stel nu dat we de niet-gecorrigeerde importquote van 74 procent invullen, dan vinden we een multiplier van 0,79. Dat is meer dan de helft lager dan 1,88 door het importlek. Maar zeker niet nul, zoals sommigen lijken te suggereren.
Als we de gecorrigeerde invoerquote invullen, dan is de bestedingsmultiplier 1,23. Ook dit is weer substantieel lager dan 1,88, maar zeker niet verwaarloosbaar. Als de overheid met 1% bbp bezuinigt, daalt het bbp met 1,2%. Dus, niet corrigeren voor de wederuitvoer en intermediaire invoer voor de export heeft substantiële effecten op de veronderstelde effectiviteit van begrotingsbeleid.
We zien dat de multiplier groter wordt als de investeringsquote stijgt: 1,40 tot 1,63. Dus als bedrijven moeite hebben hun investeringen op de markt te financieren, en dit uit eigen kasstroom moeten doen, wordt de multiplier groter.
De multiplier kan kleiner worden als mensen uit voorzorg gaan sparen. In dat geval daalt de marginale consumptiequote. De tabel geeft aan dat de bestedingsmultiplier daalt als de marginale consumptiequote zakt. Voorzorgssparen vanwege grote onzekerheid kan dus de multipliers verkleinen. Echter, aangezien sommige huishoudens in liquiditeitsproblemen zitten, kan de marginale consumptiequote oplopen, waardoor bestedingsmultipliers verder stijgen. Balansproblemen leiden dus tot grotere multipliers; als mensen financieel klem zitten worden meer euro’s aan de marge uitgegeven.
Tot slot, als de belastingen hoger zijn, nemen de multipliers natuurlijk af aangezien het belastinglek groter wordt, zie laatste regels van de tabel. Hoe dan ook, de bestedingsmultipliers liggen in dit eenvoudige modelletje altijd boven de 1 en een waarde rond 1,5 lijkt door de huidige balansrecessie waarschijnlijker.
De belastingmultipliers zijn in dit soort Keynesiaanse modellen altijd (veel) kleiner dan de uitgavenmultipliers; een belastingverlaging wordt altijd eerst voor een deel gespaard en daarmee is altijd een deel van de impuls al weggelekt, nog voordat de economie een stimulans heeft gekregen. De belastingmultiplier in een gesloten economie is -0,88. In de open economie, bij de niet-gecorrigeerde invoerquote, zou de belastingmultiplier zelfs positief worden. In dat geval is de effectieve invoerquote groter dan de marginale consumptiequote, zie de formule voor de belastingmultiplier. Dus dit toont aan dat het invoerlek inderdaad belangrijk is. De belastingmultiplier blijft voor de gecorrigeerde waarde van de invoerquote schommelen tussen de -0,1 en -0,6. Dat is niet zo hoog als de begrotingsmultiplier, maar niet zo laag dat belastingimpulsen volledig zouden weglekken naar het buitenland.
Dit simpele modelletje onderschat mogelijk de belastingmultipliers. Er is nogal wat recent empirisch bewijs dat aantoont dat ook belastingmultipliers groot kunnen zijn, zie bijvoorbeeld deze bespreking van Christina Romer.
Ter vergelijking, het CPB zelf komt opvallend genoeg op basis van haar eigen modellen tot vergelijkbare multipliers. Het CPB schat na 1 jaar een bestedingsmultiplier van 0,9 en een belastingmultiplier van -0,4.
De budget-neutrale multiplier geeft de verhoging van de productie als de overheid een bestedingsimpuls doet zonder het begrotingstekort te laten oplopen. Zoals Simon-Wren Lewis, hoogleraar macro-economie in Oxford, betoogt: ‘one is the magic number’ voor de budget-neutrale multiplier. Het nationale inkomen gaat 1-op-1 omhoog met de overheidsuitgaven, zelfs als die 100 procent gedekt zijn met hogere belastingen. En dat geldt ook in een kleine, open economie met een hoge invoerquote.
Waarom is de budget-neutrale multiplier gelijk aan 1? De reden laat zich het makkelijkst beschrijven aan de hand van de nationale inkomensidentiteit:
(S – I) = (G – T) + (E – M)
Het nationale spaaroverschot (S – I) is gelijk aan het begrotingstekort (G – T) plus het exportoverschot (E – M). Neem voor nu voor het gemak even aan dat Nederland een gesloten economie is E = M = 0. Een budget-neutrale verhoging van de overheidsuitgaven leidt niet tot een verandering van het begrotingssaldo (G – T). Dat betekent dat het netto spaaroverschot (S – I) ook niet zal veranderen. Dus S – I = (Y – T) – C(r,Y – T) – I(r,Y – T) verandert niet. Dit kan alleen als het inkomen Y precies zoveel stijgt als de belastingen T, zodanig dat het netto besteedbaar inkomen Y – T ongewijzigd blijft. De productie gaat daarom net zoveel omhoog als de overheidsuitgaven en belastingen toenemen en dus is de budget-neutrale multiplier gelijk aan 1.
Nu valt eenvoudig in te zien dat dit onverkort blijft gelden in een kleine open economie. Als het netto besteedbaar inkomen Y – T niet verandert, dan blijven ook de netto exporten ongewijzigd: E – M = E(e, Y* – T*) – M(e, Y – T). Dus blijft de nationale inkomensidentiteit opgaan als het inkomen even hard stijgt als de uitgaven en de belastingen.
Ik weet, er zijn veel geavanceerdere, moderne modellen dan dit eenvoudige IS-LM (Mundell-Fleming) model. De multiplierberekeningen kunnen daarom worden bekritiseerd. Maar de vraag is of meer complexere modellen kunnen aantonen dat begrotingspolitiek wel zinloos zou zijn door weglekeffecten naar het buitenland onder geschetste condities (korte termijn, vaste prijzen, vaste wisselkoersen, exogeen monetair beleid). Ik meen van niet. Maar ik laat me graag overtuigen van het tegendeel, op basis van theorie of empirie, en niet door ‘proof by assertion’.
Begrotingsimpulsen lekken niet volledig weg via de importen, zelfs niet in zeer open economie als Nederland. Ik hoop daarom dat dat collega-economen en andere commentatoren volgend jaar iets minder stellig zullen beweren dat weglekeffecten alle begrotingspolitiek impotent zou maken. Want dat is onjuist.
Reacties op commentaar
Naar aanleiding van de eerste blog heeft een aantal mensen gereageerd. Waarvoor grote dank. Ik heb op basis van hun commentaar mijn blog aangepast. Hieronder beschrijf ik wat ik heb veranderd.
Mathijs Bouman vroeg zich af aan welke goederen huishoudens hun geld besteden. Ik heb nu een verwijzing naar CBS bestedingsdata opgenomen.
Mathijs Bouman en Pieter Gautier vroegen zich af of het geoorloofd was om voor de marginale invoerquote de gemiddelde invoerquote in te vullen, zoals ik heb gedaan. Dat is een goede vraag. Uit CPB-schattingen blijkt dat de invoerelasticiteiten door het CPB rond de 1 worden geschat. Bij een elasticiteit van 1 zijn de gemiddelde effecten gelijk aan de marginale effecten. Dus denk ik dat de benadering redelijk goed is.
Robin Fransman en Robert Went maakten goede opmerkingen dat de invoerquote – zelfs als die wordt gecorrigeerd voor de wederuitvoer – nog een overschatting is, omdat niet wordt gecorrigeerd voor de invoer van intermediaire goederen bestemd voor de uitvoer. Dat heb ik in deze blog aangepast. Fransman suggereerde dat de effectieve invoerquote dan slechts 25 procent zou bedragen. Op basis van CBS schattingen van 2003 kom ik nu uit op 28 procent. Deze schatting zou dus mogelijk nog iets te hoog kunnen zijn.
Jaap Abbring constateerde terecht dat ik een vergissing heb gemaakt bij het invullen van de invoerquote. Ik had de geobserveerde invoerquote moeten delen door (1 – t), zie ook voetnoot [1]. Overigens gold dit eveneens voor de investeringsquote. Dit is gecorrigeerd in de nieuwe berekeningen. De schattingen voor de consumptiequote zijn gebaseerd op het besteedbare inkomen, waardoor geen correctie nodig is.
Noten
[1] In het model is marginale invoerquote ΔM/ΔY = (1 – t)m. In de CBS-data is gemiddelde invoerquote M/Y = mCBS. Als de gemiddelde invoerquote gelijk is aan de marginale invoerquote, dan geldt mCBS = (1 – t)m. Dus, in het model moet worden ingevuld m = mCBS/(1 – t). Dit geldt ook voor de investeringsquote.
[2] Het CPB schat een coëfficiënt van ongeveer 0,2 in een regressie van Δ(I/Y) op ΔY/Y (CPB, 2011). Dus geldt Δ(I/Y) = ΔI/Y – (I/Y)ΔY/Y = 0,2×ΔY/Y. Herschrijven geeft: ΔI/ΔY = 0,2 + (I/Y) ≈ 0,4.