Mismatch van leerlingen in Amsterdam (2)

Afgelopen woensdag schreef ik op deze site een blog over de matchingprocedure van leerlingen in Amsterdam. Er zijn verschillende matchingsprocedures denkbaar en dus moeten er afwegingen worden gemaakt. Dit is niet alleen een afweging tussen statistische kenmerken van de procedure, maar ook een afweging tussen verschillende groepen ouders. Op basis van een simulatie met een fictief voorbeeld laat ik hier zien hoe dit werkt.

In dit voorbeeld moeten 1000 leerlingen verdeeld worden over 10 scholen. Vijf van die scholen zijn populair, maar hebben een maximale capaciteit van 100 leerlingen. De andere vijf scholen staan minder in de belangstelling en hebben geen maximale capaciteit.

Daarnaast zijn er twee soorten ouders. Ouders van type 0 hebben één van de vijf populaire scholen als nummer 1 op hun voorkeurslijst gezet en een niet populaire school op nummer 2. Het liefst hebben zij hun kind dus op een bepaalde populaire school, maar als dat niet lukt is hun tweede keuze een andere school die niet tot de vijf populaire scholen behoort. Ouders van type 1 hebben de vijf populaire scholen als nummer 1 t/m 5 op hun voorkeurslijst staan. In een willekeurige volgorde. Ze verschillen onderling dus over welke populaire school hun voorkeur heeft, maar prefereren allemaal al deze populaire scholen boven de niet populaire scholen. Voor alle ouders is de eerste voorkeur dus een populaire school. 1000 leerlingen moeten dus over 500 plaatsen worden verdeeld. Er zou uiteraard ook een type ouder kunnen zijn met als eerste voorkeur een niet populaire school, maar die doen er voor de analyse niet toe. Hun kind zal altijd op hun eerste voorkeur worden geplaatst.

In de simulatiestudies die voor de Amsterdamse matching zijn gedaan worden twee methodes met elkaar vergeleken: RSD en DA. RSD kent één lotingslijst voor de hele stad. De leerling die het hoogste staat op deze lijst wordt als eerste aan zijn school van voorkeur toegewezen. Zo gaat men de lijst af, totdat er een leerling is bij wie de school van de eerste voorkeur vol zit. Die leerling wordt dan toegewezen aan de school die het hoogst op zijn lijst staat waar wel nog plaats is.

In mijn simulatie levert dit de volgende verdeling op.

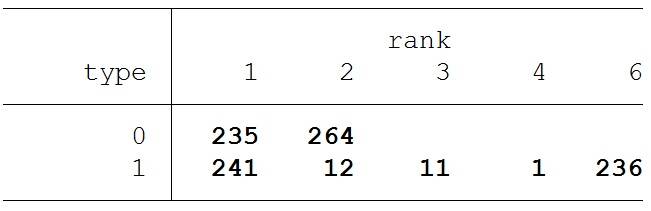
De tabel geeft per type ouder aan de hoeveelste voorkeur de toegewezen school heeft. Bij beide type ouders is in iets minder dan de helft van de gevallen de eerste voorkeur toegewezen (235 leerlingen van type 0 en 241 leerlingen van type 1 worden geplaatst op hun eerste voorkeur). Dit is net niet de helft omdat er door het toeval kleine verschillen zijn in de voorkeur voor een van de vijf populaire scholen. Sommige leerlingen moeten daarom uitwijken naar een andere school. Bij ouders van type 0 is dit altijd de tweede keuze, omdat die school immers geen capaciteitslimiet heeft. Bij type 1 komt men soms nog op een andere populaire school terecht, omdat de loting net niet goed genoeg was voor de school van de eerste voorkeur, maar net wel voor een andere populaire school. In de meeste gevallen komen deze leerlingen echter terecht op de zesde voorkeur omdat dat de eerste school zonder capaciteitsbeperking is.   

Je kunt op twee manieren naar deze verschillen kijken. Beide type ouders hebben ongeveer dezelfde kans om op een school van hun eerste voorkeur te worden geplaatst. In die zin verdeelt de procedure de schaarse plekken gelijk. Ouders van type 0 hebben echter een veel grotere kans om op een school van hun tweede voorkeur te komen. Die tweede voorkeur is bij hen, in tegenstelling tot bij ouders van type 1, echter niet schaars. Alle leerlingen hebben dus een redelijk vergelijkbare kans om op een school terecht te komen waarvoor de capaciteit beperkt is. En als ze op zo’n school komen, is het in de meeste gevallen de school van hun eerste voorkeur.

Het alternatief DA kent een aparte loting voor iedere school. Het levert de volgende verdeling op:

De kans op plaatsing op een school van de eerste voorkeur is voor beide type ouders een stuk lager. De reden hiervoor is dat een groot aantal plaatsen, voor beide typen ouders, nu worden ingenomen door leerlingen van type 1 die de betreffende school op de tweede, derde, vierde of vijfde plaats hadden staan. Leerlingen van type 0 moeten daarom vaker uitwijken naar hun tweede voorkeur. Leerlingen van type 1 komen minder vaak op hun eerste voorkeur terecht, maar in totaal wel veel vaker op één van de populaire scholen. Deze methode geeft ouders die alle populaire scholen bovenaan hun lijst hebben staan dus veel meer kans om een van de schaarse plekken te krijgen. Ouders die alleen op de eerste plaats een populaire school hebben staan, moeten veel vaker uitwijken naar een school zonder capaciteitsprobleem.

Een groot nadeel van de DA-methode is dat het in een groot aantal gevallen voorkomt dat de toegewezen school geruild zou kunnen worden. Leerling A zit op school Y, maar had liever op X gezeten, terwijl leerling B op X zit terwijl hij liever op Y had gezeten.

Als men zou toestaan dat ouders in deze gevallen gaan ruilen zou – als alle ruilmogelijkheden worden benut – de volgende verdeling ontstaan:

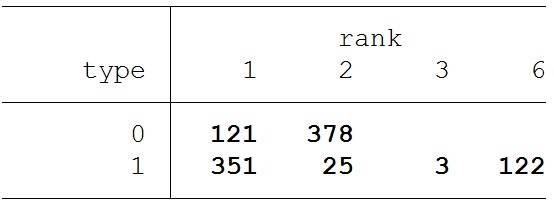
Het ruilen heeft alleen effect voor type 1. Een groot deel van deze leerlingen komt nu terecht op de school van de eerste voorkeur. Slechts enkele leerlingen gaan nog naar een andere populaire school. Door toevalligheden in de verdeling is er voor hen geen plaats op de school van de eerste voorkeur. Het ruilen heeft twee nadelen. In de eerste plaats krijgen juist de ouders van type 1, die toch al veel voordeel hadden van de DA-methode, hier nog een extra voordeel. Het verschil in uitkomsten tussen beide groepen wordt dus nog groter. Een tweede nadeel, is dat het toestaan van ruilen tot strategisch gedrag kan leiden. Voor ouders van type 0 kan het nu ook gunstig worden om alle populaire scholen hoog op de voorkeurslijst te zetten. Daarmee vergroten zij hun kans op plaatsing op een populaire school. Als dit niet de school van hun eigen voorkeur is, kunnen ze dit plaatsingsrecht ruilen voor de school die wel hun voorkeur heeft.

Als zij dit zouden doen (of als de computer hun voorkeur bij de plaatsing aanpast aan wat strategisch gunstig is, en vervolgens ruilt op basis van de echte voorkeur) dan is dit het resultaat: 

De verdeling lijkt heel sterk op de eerste verdeling waarbij RSD werd gebruikt. Dat is het bijzondere aan dit dilemma. DA is gunstiger voor ouders van type 1. Als DA wordt toegepast dan zou ruilen de uitkomst voor deze ouders nog verder verbeteren. Maar door ruilen toe te staan zal er ook strategisch gedrag ontstaan, waardoor per saldo het voordeel voor deze ouders van DA verdwijnt en zij net zo goed af zijn als bij RSD. Het niet mogen ruilen is dus een soort straf, die het mogelijk maakt om de ouders van type 1 een gunstigere plaatsing te geven en tegelijkertijd een dreiging voor ouders van type 0, die voorkomt dat zij door het strategisch invullen van hun voorkeurslijst ook een hogere kans op plaatsing op de school van eerste voorkeur krijgen.