
In het Amsterdamse middelbaar onderwijs is al jaren sprake van overaanmelding op populaire scholen. Dit jaar is voor het eerst een matchingprocedure gebruikt die voor een optimale verdeling van leerlingen over scholen moet zorgen. Naast het bericht dat deze procedure goed is verlopen, kwamen echter ook gevallen in het nieuws waarbij twee leerlingen elk waren geplaatst op de school die de voorkeur van de andere leerling had. Met een eenvoudige ruil zouden beide leerlingen dus beter af zijn. Vanwege de onvrede van de ouders kwam er zelfs een kort geding. Het is natuurlijk erg jammer dat er zulke onvrede onder de ouders is, en voor economen moet het vreemd zijn dat een matchingsprocedure tot Pareto-inefficiënte uitkomsten leidt.
De gevolgde matchingsprocedure is gebaseerd op een simulatiestudie van Pieter Gautier, Monique de Haan, Bas van der Klaauw en Hessel Oosterbeek (zie ook de blog van Pieter Gautier over dit onderwerp). De methode heet Deferred Acceptance en kan mooi geïllustreerd worden met het zoeken van een partner. Stel er zijn drie mannen A, B en C en drie vrouwen X, Y en Z. In de matrix worden de voorkeuren van deze drie mannen en drie vrouwen voor een partner van het andere geslacht weergegeven. Voor man A is vrouw X de meest aantrekkelijke partner, gevolgd door Y en dan Z. Vrouw X vindt B het aantrekkelijkst, gevolgd door C en A.
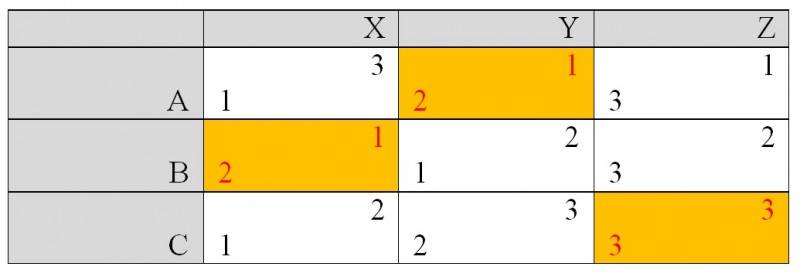
Als iedere man nu de vrouw van de eerste voorkeur voorstelt een relatie te beginnen, dan krijgt X dit verzoek van A en C en Y van B. X zal het verzoek van C accepteren – hij is voor haar immers aantrekkelijker dan A en Y zal het verzoek van B accepteren. A zit dus nog zonder partner en zal een nieuwe poging wagen bij zijn tweede voorkeur Y. Y heeft al een relatie met B, maar A is aantrekkelijker voor haar, dus maakt ze het uit met B en accepteert ze het verzoek van A. Nu is B alleen. Hij zal ook naar zijn tweede voorkeur gaan en vraagt X of zij een relatie met hem wil. B is de meest aantrekkelijke man voor X, dus zij zegt ja, waardoor vervolgens C weer op zoek moet naar een nieuwe partner. Zijn tweede voorkeur Y zal nee zeggen zodat hij uiteindelijk een relatie met Z zal krijgen. De gekleurde cellen zijn de koppels die uiteindelijk gevormd worden: A met Y, B met X, C met Z.
Opmerkelijk is dat A liever partner X had gehad en B Y. Ruilen is echter geen optie, want X en Y zouden niet akkoord gaan. Voor hen zijn Y en X immers de ideale partners. Het is uit de literatuur bekend dat deze matchingsmethodiek altijd leidt tot een stabiele matching. Er kunnen geen nieuwe koppels gevormd worden waarbij de twee partners beter af zijn dan met hun huidige matching. Bovendien, zo is aangetoond in de literatuur, is er voor mannen in dit proces geen voordeel te behalen uit strategisch gedrag, door niet gewoon in de volgorde van voorkeur de vrouwen langs te gaan. Ze kunnen dus gewoon eerlijk zijn.
Deze aanpak is ook door Amsterdam gevolgd. Een groot verschil met de levenspartners is dat de Amsterdamse scholen geen voorkeur voor leerlingen hebben (of eigenlijk niet mogen hebben). Om de methode toch te kunnen gebruiken is daarom voor iedere school een loting gedaan, waarmee een artificiële rangorde van de leerlingen voor elke school is gemaakt. In de matrix zijn A, B en C nu leerlingen die op school X, Y of Z terecht kunnen komen. De voorkeur van de scholen is de uitslag van de loting.
Deze kleine aanpassing maakt echter een groot verschil. Leerling A zou immers liever naar school X gaan en leerling B naar school Y. In tegenstelling tot vrouwen hebben deze scholen geen echte voorkeur. Hun voorkeur is alleen de uitslag van de loting. Nu zou een ruil dus wel mogelijk zijn. Als A en B van school ruilen zijn ze beide beter af, zonder dat dit nadelige consequenties voor de scholen heeft. In een interview met Parool in 2012 kondigde Pieter Gautier nog aan dat de nieuwe aanpak “leidt tot ‘stabiele matching’; scholieren zullen niet met elkaar van plek willen ruilen.” Dit laatste blijkt dus wel het geval te zijn. Volgens de berichten komen dergelijk situaties veel voor. Vandaar dat de ouders vinden dat ze alsnog moeten kunnen ruilen. De onderzoekers zijn het hier niet mee eens. Als ruilen wordt toegestaan dan ontstaan er in tegenstelling tot de huidige methode, mogelijkheden voor strategisch gedrag. Door enkele heel populaire scholen hoog in de ranking op te nemen, ook als die niet de persoonlijke voorkeur hebben, is de kans groot dat men toegelaten wordt op een school die ruilmogelijkheden zal geven. De onderzoekers zien deze niet Pareto-optimale toewijzingen daarom als de prijs voor een verdeling van leerlingen over scholen die verder veel beter is dan het systeem dat er was.
Een alternatief zou zijn om voor alle scholen eenzelfde ranking van leerlingen te maken. Een dergelijke methode heet Random Serial Dictatorship (RSD). Het komt er dan op neer dat leerlingen in de volgorde van de loting hun school mogen kiezen. Als in het voorbeeld hierboven de ranking onder X voor alle scholen zou worden gehanteerd zou leerling B op school Y terecht komen, vervolgens leerling C school X kiezen en ten slotte leerling A op school Z komen. Voordeel van RSD is dat deze mogelijkheden om te ruilen niet meer zullen ontstaan. De methode is Pareto efficiënt. Maar voor leerling A zou dit niet gunstiger zijn. In plaats van dat er een ruil mogelijk is tussen de school van zijn tweede keuze waarop hij is geplaatst met leerling B op de school van zijn eerste keuze, komt hij nu op de school van zijn derde keuze. Voor C is dit overigens wel gunstiger.
Een mogelijk nadeel van RSD is dat het voor een kleine groep leerlingen tot een zeer ongunstige plaatsing kan leiden. Als een leerling in een buurt woont waar alle scholen te kampen hebben met overaanmeldingen en hij loot per toeval een heel erg lage ranking, dan zal geen van deze scholen hem toelaten en zal hij ver uit de buurt naar een school moeten gaan. Doordat bij DA iedere school een eigen loting heeft is de kans veel kleiner dat deze leerlingen bij alle scholen in zijn buurt een lage ranking krijgt en kan hij dus in iedere geval naar één van deze scholen in de buurt gaan. Om die reden is in Amsterdam voor DA gekozen.
De genoemde simulaties laten zien dat de RSD-aanpak gemiddeld tot een hogere waardering van de school waarop men wordt geplaatst leidt dan de DA-aanpak en de aanpak die vroeger werd gevolgd. Ook het percentage leerlingen dat geplaatst wordt op de eerste voorkeur is hoger. Alleen is het percentage leerlingen dat niet op de eerste, tweede of derde voorkeur wordt geplaatst is lager. Het is onduidelijk wat dit precies betekent. Dit zouden leerlingen kunnen zijn waarvan de ouders vooral heel populaire scholen in de top vijf hebben gezet. Het DA-algoritme maakt, omdat er voor iedere school afzonderlijk wordt geloot, de kans groter dat deze leerlingen op één van deze scholen worden geplaatst en zou daarmee deze groep een veel grotere kans hebben gegeven op plaatsing op een populaire school dan mensen die maar één zo’n school hoog in hun ranking hebben gezet. Maar het kan ook zijn dat het hier gaat om leerlingen die ver van waar ze wonen, naar school moeten gaan. Een goede empirische analyse van de gevolgen van verschillende plaatsingsmechanismen zou dus waardevol zijn.
Bij de keuze van de plaatsingsprocedure moeten dus afwegingen worden gemaakt. Er zijn drie aspecten die daar een rol bij spelen: (1) Is de plaatsing efficiënt in de zin dat verbetering door ruilen niet meer mogelijk is, (2) worden niet te veel leerlingen heel zwaar getroffen door de procedure in vergelijking met anderen en (3) laat de procedure ruimte voor strategisch gedrag van ouders. Het volledig uitsluiten van strategisch gedrag lijkt de grootste prioriteit te zijn geweest van de onderzoekers. Zowel DA als RSD zijn procedures die strategisch gedrag niet belonen. De vraag is of dat inderdaad het belangrijkste criterium moet zijn. Mij lijkt efficiëntie veel belangrijker, zowel om economische redenen, als omdat het aan ouders niet te verkopen valt dat de buurjongen naar de school gaat die zij voor hun eigen zoon in gedachten hadden terwijl hun zoon juist naar de school gaat waar de buurjongen heen had willen gaan. Het lijkt me dan ook niet meer dan logisch om de computer na de loting eventuele Paretoverbeteringen te laten maken tot dat Pareto-optimaliteit is bereikt. Mocht dat het gevaar oproepen van strategisch gedrag, dan kan gezocht worden naar een aanpassing van de regels die die ruimte kleiner maken. RSD is in ieder geval als alternatief achter de hand. Amsterdam beschikt nu over de data over hoe de ouders hun keuze maken. Op grond daarvan kan empirisch worden onderzocht hoe groot eventueel ongewenste gevolgen zijn, zodat, als dat nodig is, gezocht kan worden naar praktische oplossingen om deze negatieve gevolgen kleiner te maken. Ook als zulke aanpassingen niet 100% strategieproof zijn, lijkt me dat een uitruil die toch zeker overwogen kan worden.
Als het inderdaad mogelijk is om volgend jaar een aangepaste methode te introduceren die een goed matching oplevert zonder dat er mogelijkheden voor ruil overblijven, dan zou dit jaar gewoon geruild kunnen worden. De reden om dit niet te doen is immers dat dit aanleiding kan zijn voor strategisch gedrag. Dit jaar hebben de ouders hun voorkeuren al ingeleverd en volgend jaar zouden die mogelijkheden er, bij een nieuwe procedure, niet of nauwelijks meer zijn. Dit jaar zou achteraf ruilen dus eenmalig toegelaten kunnen worden. Mooi voor de ouders en mooi voor economen, voor wie het toch lastig moet zijn om een procedure te hebben die niet Pareto-optimaal is.
Auteur
Categorieën