Suggesties voor de economische inschatting van de optimale dijknormering

• Koks Husby (2018) ESB 4759 108-111.pdf Download [10,79 mb]

Voor het Deltaprogramma 2015 zijn er nieuwe waterveiligheidsnormen opgesteld, die de gewenste hoogte en sterkte van de ­dijken vaststellen. Een belangrijke basis voor deze normen zijn de kosten-batenanalyses, waarbij er uitgebreid is gekeken naar de ­verschillende factoren achter de risico’s van de economische ­schade. Hoe kan de optimale dijkhoogte nog beter ingeschat ­worden?

De manier waarop waterveiligheidsnormering bepaald worden is constant aan verandering onderhevig. Door de meest recente kennis zijn deze nieuwe normeringen nu niet meer alleen gebaseerd op de kans dat een waterkering oftewel dijk niet bestand is tegen bepaalde waterstanden en golven (de overschrijdingskans), maar ook op de gevolgen van de overstroming zelf, de blootstelling van economische objecten zoals gebouwen en de kwetsbaarheid van personen (het overstromingsrisico).

Het gevolg van deze nieuwe normeringswijze is dat er verschillende veiligheidsniveaus bestaan, afhankelijk van de eigenschappen van specifieke regio’s. De eisen vanuit de basisveiligheid stellen dat bij het bepalen van deze nieuwe normeringen de kans op overlijden van 10–5 per jaar in geen enkel gebied overschreden mag worden, en dat in het beginsel alle gebieden meetellen. Maar, in sommige gebieden is, vanuit een kosten-batenperspectief, een hoger veiligheidsniveau wenselijk. Voor deze gebieden wordt het optimale dijkbeschermingsniveau berekend aan de hand van een optimalisatie, waarbij de beschermingskosten en de geschatte overstromingsschade binnen een dijkring geminimaliseerd worden (Eijgenraam et al., 2016; Kind, 2014).

Verder is de berekening nu ook accurater omdat deze gedaan wordt per dijktraject, en niet meer voor de volledige dijkring. Het werk achter deze berekeningen (Maatschappelijke Kosten-batenanalyse Waterveiligheid 21e eeuw, WV21) vormt, door de incorporatie van de gevolgen, een significante verbetering ten opzichte van de voorgaande aanpak.

Ondanks de verbeteringen zijn er nog grote onzekerheden in de ramingen van de optimale overstromingskansen: uit een Monte Carlo-analyse, samengevat in Deltares (2011), blijkt dat de bandbreedtes rondom deze geschatte kansen variëren van −60 tot 100 procent. Onzekerheden over de totale schade die een overstroming kan veroorzaken, is over het algemeen de belangrijkste verklaring achter deze grote bandbreedte. Wegens de lange tijdshorizon van de ramingen stapelen onzekerheden rondom economische groei zich hier op (Gauderis et al., 2013).

Hoewel het werk achter deze studies indrukwekkend is en de verwachte schade steeds effectiever in kaart gebracht wordt, stellen wij dat er met het oog op de toekomst nog mogelijkheden zijn voor een betere raming. Op nog zeker twee vlakken zijn er mogelijkheden tot verder economisch onderzoek, namelijk omtrent de manier waarop zowel de totale economische gevolgen als de regionale economische groei in de modellen meegenomen worden. In dit artikel geven we suggesties hoe nieuwe ontwikkelingen binnen het regionaal economisch vakgebied nieuwe inzichten kunnen bieden aangaande de huidige kosten-batenmethodiek.

De huidige methodiek

Om het overstromingsrisico binnen een dijkring te bepalen worden er berekeningen uitgevoerd met behulp van het Hoogwater Informatie Systeem – Schade- en Slacht­offermodule (HIS-SSM) en vastgelegd in het project Veiligheid Nederland in Kaart (VNK2). De economische schade die een regio treft bij een overstroming wordt, met behulp van het HIS-SSM bepaald door overstromingskaarten aan landgebruik en economische objecten te koppelen. Dit wordt gedaan op basis van schadecurves, die de hoogte van het water wanneer het land onderloopt (de inundatiediepte, op de horizontale as) koppelen aan een schadefactor (op de verticale as) die oploopt van 0 tot 1. Om de schade van het object te berekenen, wordt vervolgens deze schade­factor vermenigvuldigd met de maximaal mogelijke schade voor dit object. Daarna worden alle berekende schades ­binnen de dijkring opgeteld om tot een totaalbedrag te komen. Door dit voor verschillende overstromingsscenario’s te doen met verschillende herhalingstijden – het gemiddelde tijdsinterval waarin de overstroming een bepaalde grenswaarde overschrijdt – kan het overstromingsrisico binnen een dijkring bepaald worden, dus de gemiddelde jaarlijkse schade die overstromingen veroorzaken.

Wanneer het overstromingsrisico bekend is, kan er vervolgens een efficiënte dijkhoogte worden berekend door voor elk dijktraject de som van de langetermijn­investeringskosten voor bescherming en de verwachte overstromingsschade te minimaliseren (Eijgenraam et al., 2016; Kind, 2014). De verwachte overstromingsschade in jaar t wordt dan als volgt berekend:

\((1) \quad Verwachte\; overstromingsschade_t =\)

\(Overstromingskans_t × Potentiële\; schade_t\)

Hierbij is de overstromingskans een functie van de ­initiële overstromingskans en dijkverhogingen tot en met jaar \(t\). De potentiële schade is een functie van de ­initiële schade en de economische groei tot en met \(t\). Hieruit volgt dan dat, voor een grote \(T\) (een eindjaar ver in de toekomst), de economische groeivoet een belangrijke veroorzaker is van de potentiële schade. De netto contante waarde (NCW) van de investering in de dijkbescherming kan berekend worden als de som van investeringskosten en de gedisconteerde schade (Fankhauser et al., 1999):

\((2) \quad NCW\; Dijkbescherming =\)

\(Σ^T_{t=0} (Investeringskosten_t +\)

\(Gedisconteerde\; verwachte \;overstromingsschade_t)\)

De onzekerheden omtrent economische waarden en groei die in de modellen gebruikt worden om het optimale niveau van bescherming te bepalen, zijn vaak echter groot (Van Dantzig, 1956). Een van deze essentiële parameters waarover onzekerheid bestaat, is de economische groei in de toekomst bij het bepalen van de investeringskosten.

De groeivoet

Economische groei is een belangrijke factor voor de optimale dijkhoogte: een toename in de waarde van beschermde gebieden kan een investering in hogere of sterkere ­dijken rechtvaardigen. Er is dan immers meer waarde om te beschermen.

De studie van Eijgenraam et al. (2016) laat zien hoe economische groei in een kosten-batenanalyse kan worden opgenomen om de optimale dijkhoogte te bepalen. Deze focus op de invloed van economische groei op de waterveiligheidsnormering is een vernieuwing ten opzichte van eerdere modellen, zoals gebruikt in Van Dantzig (1956). In de studie van Eijgenraam et al. (2016) wordt een exogene groeivoet gebruikt, die “een algemeen geaccepteerd basisscenario voor economische groei en klimaatverandering” weergeeft. Dit is een aanname die niet ongebruikelijk is in dergelijke studies. Ons inziens is het nuttig om de aanname van deze exogene groeivoet te nuanceren.

Om te beginnen zijn de resultaten van het optimalisatie-model erg gevoelig voor de waarde van deze groeivoet. Met name door het effect van de samengestelde groei en de lange levensduur van dijken kunnen kleine veranderingen een grote invloed hebben op het optimale veiligheidsniveau. In het model is economische groei dan ook een van de belangrijkste veroorzakers van onzekerheden wat betreft de optimale overstromingskans (Gauderis et al., 2013).

Dit brengt ons bij twee belangrijke vragen om deze exogene economische groei te kunnen nuanceren. De ­eerste vraag hierbij is van empirische aard: wat betekent het veiligheidsniveau voor de economische groei? De regionaal-­economische literatuur suggereert dat fundamentele veranderingen aan de omgeving, zoals veranderingen in het overstromingsrisico, een effect op de bevolkingsspreiding en economische activiteit kunnen teweegbrengen (zie ­Redding (2010) voor een overzicht).

De gevolgen van de uitval van kritieke infrastructuur kunnen veel verder reiken dan het getroffen gebied

Intuïtief lijk het ook plausibel dat bijvoorbeeld bedrijven in de Rotterdamse haven het overstromingsrisico meenemen in hun investeringsbeslissingen, en dat het bouwen van een dijk een reeks van andere effecten op de lokale economie kan hebben. De vraag is dan of deze effecten tijdelijk of permanent zijn: tijdelijke groeifluctuaties hebben immers weinig effect op langetermijnbeslissingen, zoals beslissingen over optimale dijkbescherming. In een recent artikel vonden wij een permanent positief effect op de bevolkingsgroei na de constructie van de Deltawerken (Husby et al., 2014). Hierin konden we echter niet de oorzaken van deze positieve effecten achterhalen. De implementatie van de Delta­werken heeft ongetwijfeld ook andere effecten op de lokale economie gehad, naast de reductie van het overstromingsrisico (zoals bijvoorbeeld een verbeterde ontsluiting door wegen over de stormvloedkeringen). Toekomstig onderzoek zou zich kunnen richten op de invloed op grond­gebruik en economische productie van de Deltawerken.

Stel dat empirische studies laten zien dat veiligheid een effect op de economische groei heeft, dan is de groeivoet niet exogeen maar endogeen. Dit leidt tot een tweede vraag, van meer theoretische aard: wat betekent endogene economische groei voor de optimale dijkhoogte? Dit vergt een toevoeging aan het model (dat in Eigenraam (2016) beschreven is): een randvoorwaarde waarin in elke periode de groeivoet afhankelijk is van hoe hoog de dijk is. Als eerste benadering kunnen we de relatie tussen groei en hoogte specificeren als een functie met een afnemende stijging. In dat geval is de verandering in economische groei die het gevolg is van een hogere dijk groter bij lage dan bij hoge veiligheidsniveaus. En door een functie met afnemende stijging te gebruiken, heeft een verlaging van het veiligheidsniveau een groter absoluut effect op de groei dan een verhoging van dezelfde grootte. In een model met endogene groei wordt dus potentiële schade gekoppeld aan veiligheid, met een interessante trade-off voor beleid. Aan de ene kant leidt een dijkverhoging namelijk tot een verminderde overstromingskans, en daarbij tot een reductie in de verwachte schade. Maar aan de andere kant leidt een dijkverhoging ook tot een grotere economische groei en daarbij een hogere potentiële schade (Haer et al., 2016).

Bovenregionale effecten en de (on)afhankelijkheid van regio’s

Om het overstromingsrisico binnen een dijkring te bepalen, wordt er in HIS-SSM gebruikgemaakt van een opslagfactor om de indirecte gevolgen van een overstroming te bepalen. Het HIS-SSM definieert deze indirecte gevolgen als “de schade bij toeleverende en afnemende bedrijven buiten het dijkringgebied vanwege het (deels) wegvallen van omzet en de schade vanwege het doorsnijden van aan- en afvoerroutes” (Gauderis, 2009). Deze verliezen worden in de totale geschatte schade meegenomen door de directe schade altijd met een factor 1,5 te vermenigvuldigen (­Deltares, 2011). Hierbij wordt er uitgegaan van het idee dat de indirecte effecten voor elke regio tot vergelijkbare netto negatieve gevolgen zullen leiden.

De aanwending van een dergelijke opslagfactor in de berekening van het overstromingsrisico is niet ongebruikelijk. Het Britse equivalent van HIS-SSM, de Multi-­Coloured Manual (MCM), gebruikt bijvoorbeeld een soortgelijke aanpak (Penning-Rowsell et al., 2005). Bij het toepassen van een vaste opslagfactor worden echter twee impliciete aannames gedaan. Ten eerste wordt er aangenomen dat elke regio een vergelijkbare economische structuur heeft. Ten tweede neemt men aan dat het economisch herstel van de regio bij elke overstroming en in elke regio ­vergelijkbaar is, ongeacht de herhalingstijd.

Er is één belangrijke reden waarom deze manier van overstromingsschade berekenen tot een suboptimale bepaling van de totale economische gevolgen kan leiden. Dat is het feit dat de Nederlandse economie divers is (figuur 1) en er een duidelijke geografische ordening is qua type economieën binnen Nederland (CBS, 2015). Met andere woorden, er is een relatief grote variatie in economische structuur tussen de verschillende provincies en, in het verlengde daarvan, tussen de dijkringgebieden.

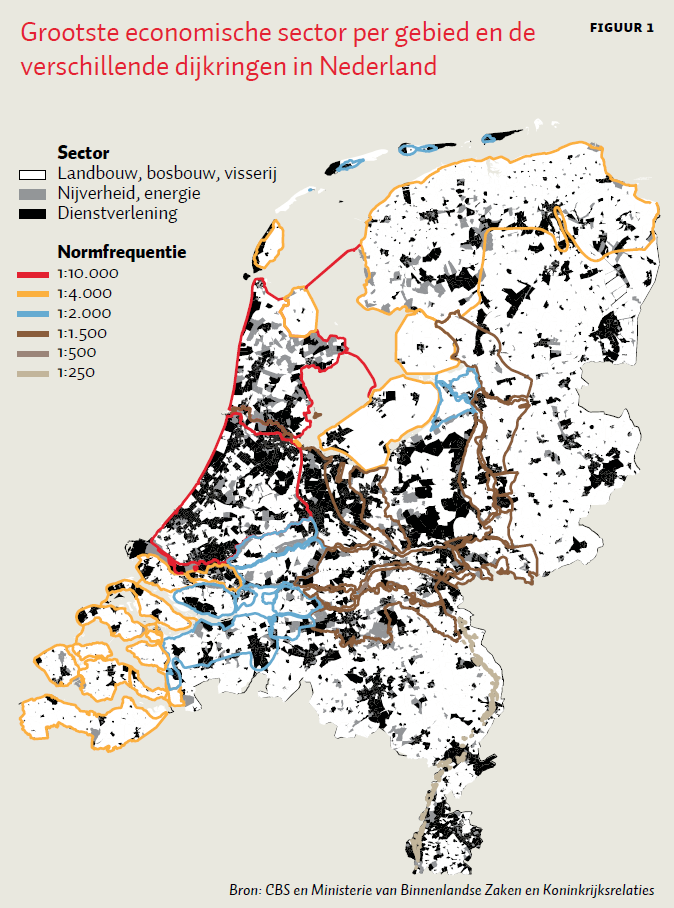
Dit betekent dat binnen Nederland de indirecte ­effecten ook zullen variëren. Een dijkringgebied met een voornamelijk agrarische economie (dijkring 6, Friesland en Groningen) herstelt zich niet alleen anders dan een regio met bijvoorbeeld een dominante financiële sector (dijkring 14, Zuid-Holland), maar de afhankelijkheden en handel wat betreft andere regio’s – zowel binnen als ­buiten Nederland – zullen ook significant verschillen doordat diverse economieën uiteenlopende vormen van handel hebben. Een overstroming binnen dijkring 53 (regio Zwolle), een dijkringgebied waar voornamelijk lokale en regionale ­handel plaatsvindt, zal zorgen voor aanzienlijk lagere bovenregionale gevolgen dan bijvoorbeeld een overstroming binnen dijkring 44, waarin Amsterdam Westpoort zich bevindt. Binnen dijkring 53 zal een lagere factor om de indirecte schade te schatten dus meer recht doen aan de werkelijkheid.

De totale bovenregionale gevolgen worden sterk beïnvloed door de mogelijkheden van substitutie en overname van productie in niet-getroffen regio’s. Koks en Thissen (2016) laten bijvoorbeeld zien dat bij een overstroming met een kans van 1:10.000 de economische verliezen 36 procent lager zijn in de getroffen regio bij het gebruik van een multiregionaal model, waarbij ook het effect op omliggende regio’s wordt meegenomen, in vergelijking met een model waarin alleen wordt gekeken naar de indirecte gevolgen in de regio zelf (Koks et al., 2015).

Voor een betere inschatting van overstromingsrisico’s zou, zoals ook wordt aanbevolen in Gauderis (2009), het raamwerk dat gebruikt wordt (HIS-SSM), moeten worden uitgebreid met een structureel (multi)regionaal-­economisch model, zoals de in de wetenschappelijke literatuur al vaak toegepaste input-output en algemeen-evenwichtsmodellen (Hallegatte, 2008; Okuyama en Santos, 2014). Hiermee kan de bandbreedte van de onzekerheid rondom de opslagfactor van 1,5 deels gereduceerd worden en de interpretatie van de risicoschattingen verbeterd worden.

Een andere belangrijke reden om te pleiten voor een meer (multi)regionaal-economische aanpak is dat de uitval van vitale en kritieke infrastructuur veel verder kan reiken dan het getroffen gebied. Daarbij gaat het bijvoorbeeld om elektriciteitscentrales, nutsvoorzieningen en ziekenhuizen, die ook buiten de dijkring diensten leveren.

Bedrijven die buiten het overstroomde gebied zonder stroom zitten, kunnen voor een aanzienlijke toename in de totale verliezen zorgen. Om de economische gevolgen van de elektriciteitsuitval te berekenen, zijn de traditionele overstromingsrisico-modellen niet toereikend. Er zijn buiten het overstroomde gebied immers geen objecten kapot, ze zijn alleen buiten gebruik. Een voorbeeld hiervan is de uitval van het 380 kV-station in Diemen op 27 maart 2015. Dit had verstrekkende gevolgen in meerdere regio’s, terwijl er nauwelijks fysieke schade was. Om deze bovenregionale gevolgen beter in te schatten, is het nodig om alternatieve modellen te gebruiken, zoals regionaal-economische modellen.

Conclusies

Het huidige model om in Nederland de optimale water­veiligheidsnormen te bepalen is een state-of-the-art-model en een internationale koploper in het vakgebied. Geen enkel model of methode is ooit compleet, en daarom hebben wij in dit artikel twee vragen naar voren gebracht waarvoor we beargumenteerd hebben dat er ruimte is voor ­verder economisch onderzoek.

Ten eerste kan verder onderzoek zich richten op de groeivoet van de economische activiteit binnen een dijkring (de blootstelling). Ons voorstel is om de relatie tussen economische groei en veiligheid beter in kaart te brengen. Door het effect van de samengestelde groei en het lange tijdsperspectief van de schattingen kunnen kleine veranderingen grote invloed hebben op het optimale niveau van veiligheid. Een endogene groeivoet heeft dus mogelijk een grote impact op het optimale veiligheidsniveau.

Ten tweede stellen wij voor om het raamwerk voor de bepaling van het overstromingsrisico (HIS-SSM) uit te breiden met een structureel (multi)regionaal-economisch model, zoals bijvoorbeeld dat van Hallegatte (2008) of Koks en Thissen (2016). Dergelijke modellen zijn ook waardevol om de bovenregionale gevolgen van de uitval van kritieke infrastructuur in kaart te brengen en om de ­mogelijkheden van alternatieve ‘zachte’ adaptatiemaat­regelen te verkennen. Een verbeterde infrastructuur voor een versneld herstel kan zorgen voor lagere indirecte gevolgen (de duur van de uitval zal immers gereduceerd ­worden). Om deze maatregelen te kwantificeren zijn echter economische modellen noodzakelijk.

Literatuur

CBS (2015) De regionale economie, 2014. Den Haag/Heerlen: CBS.

Dantzig, D. van (1956) Economic decision problems for flood prevention. Econometrica, 24(3), 276–287.

Deltares (2011) Maatschappelijke kosten-batenanalyse Waterveiligheid 21e eeuw. 1204144-006-ZWS-0012, 31 maart 2011. Publicatie te vinden op edepot.wur.nl.

Eijgenraam, C., R. Brekelmans, D. den Hertog en K. Roos (2016) Optimal strategies for flood prevention. Management Science, 63(5), 1644–1656.

Fankhauser, S., J.B. Smith en R.S. Tol (1999) Weathering climate change: some simple rules to guide adaptation decisions. Ecological Economics, 30(1), 67–78.

Gauderis, J. (2009) Schade ten gevolge van productie-uitval bij overstromingen. Discussienotitie in het kader van de KBA Waterveiligheid 21e eeuw. Rotterdam; Rebel Advisory Group.

Gauderis, J., J. Kind en R. van Duinen (2013) Robustness of economically efficient flood p­rotection standards: Monte Carlo analysis on top of cost-benefit analysis. In: F. Klijn en T. Sweckendieck (red.), Comprehensive flood risk management. Londen: Taylor & Francis, 851–858.

Haer, T., W.J. Botzen, H. de Moel en J.C. Aerts (2017) Integrating household risk mitigation behavior in flood risk analysis: an agent-based model approach. Risk Analysis, 37(10), 1977–1992.

Hallegatte, S. (2008) An adaptive regional input-output model and its application to the assessment of the economic cost of Katrina. Risk Analysis, 28(3), 779–799.

Husby, T.G., H.L. de Groot, M.W. Hofkes en M.I. Dröes (2014) Do floods have permanent effects? Evidence from the Netherlands. Journal of Regional Science, 54(3), 355–377.

Kind, J.M. (2014) Economically efficient flood protection standards for the Netherlands. Journal of Flood Risk Management, 7(2), 103–117.

Kind, J.M., S. Reinhard, A. Wooning en P.J. Zwaneveld (2014) MKBA’s voor waterveiligheid en zoetwater. ESB, 99(4696S), 68–73.

Koks, E.E. en M. Thissen (2016) A multiregional impact assessment model for disaster analysis. Economic Systems Research, 28(4), 429–449.

Koks, E.E., M. Bočkarjova, H. de Moel en J.C. Aerts (2015) Integrated direct and indirect flood risk modeling: development and sensitivity analysis. Risk Analysis, 35(5), 882–900.

Okuyama, Y. en J.R. Santos (2014) Disaster impact and input–output analysis. Economic ­Systems Research, 26(1), 1–12.

Penning-Rowsell, E., C. Johnson, S. Tunstall et al. (red.) (2005) The benefits of flood and coastal risk management: a handbook of assessment techniques. Londen: Middlesex University Press.

Redding (2010) The empirics of new economic geography. Journal of Regional Science, 50(1), 297–311.