MMT door de lens van het IS-LM-model

• Jacobs, B. (2021) ESB, 106(4796), 180-183. Download [266,54 kb]
• Jacobs, B. (2021) ESB, 106(4796), online bijlage Download [221,53 kb]

Een formele, modelmatige uitwerking van Moderne Monetaire Theorie ontbreekt, waardoor deze theorie niet wordt begrepen en er spraakverwarring ontstaat. Ook is de toepassing van deze theorie in beleid en onderwijs problematisch. Analyse van een drietal belangrijke MMT-claims met het IS-LM-model toont dit aan.

Moderne Monetaire Theorie (Modern Monetary Theory, MMT) is een theorie van overheidsfinanciën (Kelton, 2020; Mitchell et al., 2019; Wray, 2012). Ze stelt dat een overheid met een eigen munt geen financiële beperkingen kent en al haar uitgaven altijd monetair kan financieren. De enige beperking aan het gebruik van monetaire financiering is oplopende inflatie, maar dat kan worden voorkomen door de belastingen te verhogen.

MMT krijgt enerzijds steeds grotere politieke en maatschappelijke invloed, maar leidt anderzijds ook tot een alsmaar grotere spraakverwarring over wat de theorie precies inhoudt. MMT is een intellectuele incarnatie van Lerners theorie van ‘functionele financiering’ (Lerner, 1943), die stelt dat het budgettaire en monetaire beleid alleen moet worden beoordeeld op het realiseren van volledige bezetting en werkgelegenheid.

Artikelen over MMT kunnen in de meeste vooraanstaande economietijdschriften niet worden aangetroffen, op een kritische bespreking van Mankiw (2020) na. MMT’ers schrijven vooral voor eigen parochie in heterodoxe tijdschriften. Het vinnige debat tussen mainstream-economen en MMT’ers vindt vooral via blogs, opinie-artikelen en werkdocumenten plaats.

Een groot probleem is dat MMT’ers vooralsnog weigeren om hun verstrekkende claims te onderbouwen met economische modellen. Verschillende economen interpreteren de MMT als het IS-LM-model (Investments-Saving en Liquidity preference-Money supply) met een horizontale LM-curve (‘liquiditeitsval’) en een verticale IS-curve, zodat de bestedingen niet afhangen van de rente (DeLong, 2019; Jayadev en Mason, 2018; Rowe, 2011; Wren-Lewis, 2016). Maar iedere econoom die probeert MMT te analyseren met concepten uit de mainstream-economie krijgt het verwijt de theorie niet te hebben begrepen (Kelton, 2019; Wray, 2021).

Zolang een modelmatige onderbouwing van MMT ontbreekt, kunnen studenten, beleidsmakers en docenten economie niet op een logisch-consistente wijze inzicht krijgen in de wonderlijke economie van MMT. Dat inzicht is voor een goed begrip wel noodzakelijk. In dit artikel worden daarom met het IS-LM-model drie prominente MMT-claims geanalyseerd, namelijk dat rentes altijd dalen na een monetair gefinancierde begrotingsexpansie, hoe toepassing van MMT-beleidsprincipes inflatie kan voorkomen, en dat MMT breekt met de inzichten van de mainstreameconomie, en daarmee zorgt voor een ‘copernicaanse wending’ in het macro-economische denken (Kelton, 2020).

IS-LM-model

Om de diverse claims van MMT te begrijpen, analyseert dit artikel een vereenvoudigd, lineair IS-LM-model voor een gesloten economie (Hicks, 1937; Keynes, 1936). Het inkomen of bruto binnenlands product (bbp) is gelijk aan Y. De nominale rente is i. Het prijspeil is P en is op korte termijn constant.

De consumptie is een lineaire functie \(C = C_0 + c(Y − T) − ai\). \(C_0\) is de autonome consumptie en \(T\) zijn de belastingen. De consumptie stijgt als het netto besteedbaar inkomen \(Y − T\) stijgt en daalt als de rente stijgt. \(c\) is de marginale consumptiequote, en ligt tussen nul en één (\(0 < c < 1\)). \(a > 0\) is de rentegevoeligheid van de consumptie. De investeringen \(I = I_0 − bi\) dalen als de rente stijgt. \(I_0\) zijn de autonome investeringen, en \(b > 0\) is de rentegevoeligheid van de investeringen. De overheidsuitgaven \(G\) zijn autonoom. De IS-curve geeft de combinaties van het inkomen en de rente, waarbij de goederenmarkt in evenwicht is:

\(Y = m(C_0 + I_0 + G − cT) − fi\). (1)

De bestedingsmultiplier is gelijk aan \(∂Y/∂G = m ≡1/(1 − c) > 1\). De belastingmultiplier is gelijk aan \(∂Y/∂T = −cm = −c/(1 − c) < 0\). Verder meet \(f ≡ (a + b)/(1 − c)\) de rentegevoeligheid van de geaggregeerde vraag.

Evenwicht op de geldmarkt wordt beschreven door de LM-curve, en wordt bepaald door de gelijkheid van de reële geldvraag \(L\) en het reële geldaanbod \(M/P\). Het nominale geldaanbod \(M\) wordt bepaald door de centrale bank. De reële geldvraag is een lineaire functie van het inkomen en de rente: \(L = gY − hi\). De geldvraag neemt toe als het inkomen stijgt, en daalt als de rente stijgt (\(g > 0\) en \(h > 0\)). De LM-curve geeft de combinaties van het inkomen en de rente, waarbij de geldmarkt in evenwicht is:

\(M/P = gY − hi\). (2)

Effect overheidsuitgaven op rente ambigu

Een belangrijke claim van MMT is dat een toename van de overheidsuitgaven altijd leidt tot een lagere rente (Kelton, 2020, p. 120) en daarmee private consumptie en investeringen aanmoedigt in plaats van verdringt, zoals in de mainstream economische theorie.

In het IS-LM-model is het duidelijk dat een toename van de overheidsuitgaven nooit leidt tot een lagere rente indien die wordt gefinancierd door grotere begrotingstekorten, zie figuur 1. Hogere overheidsuitgaven leiden tot een verschuiving van de IS-curve naar rechts van \(\textrm{IS}_0\) naar \(\textrm{IS}_1\). Echter, de inkomensstijging leidt ook tot een hogere geldvraag waardoor de rente stijgt. Een deel van de hogere overheidsuitgaven wordt aldus verdrongen door een lagere consumptie en investeringen (verschuiving over de \(\textrm{IS}_1\)-curve naar links). Verdringingseffecten zijn groter als de rentegevoeligheid van de bestedingen \(f\) groter wordt. Hogere overheidsuitgaven leiden op de korte termijn dus altijd tot een stijging van het inkomen (van \(Y_0\) naar \(Y_1\)) en een stijging van de rente (van \(i_0\) naar \(i_1\)).

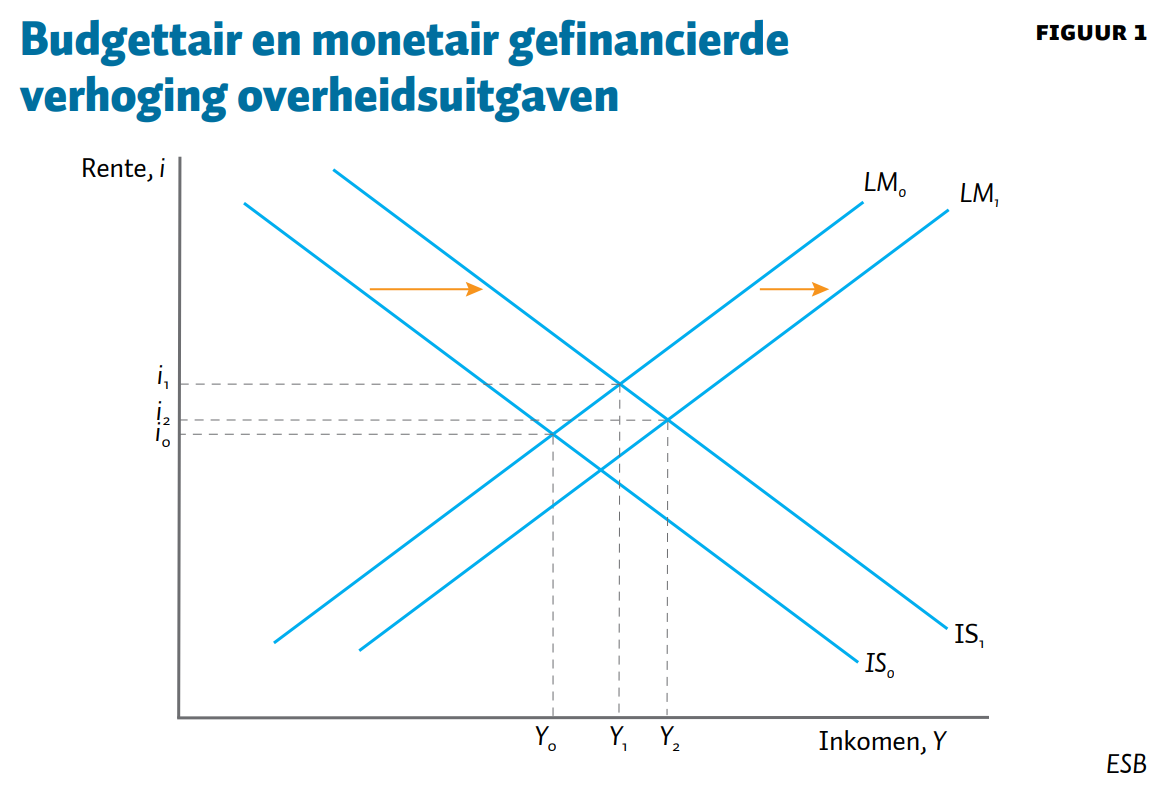
In MMT worden hogere overheidsuitgaven altijd monetair gefinancierd. Er gebeuren dan twee dingen: de IS-curve verschuift naar rechts van \(\textrm{IS}_0\) naar \(\textrm{IS}_1\), zoals ook het geval zou zijn bij budgettaire financiering. Maar daarnaast schuift ook de LM-curve naar rechts vanwege de monetaire expansie van \(\textrm{LM}_0\) naar \(\textrm{LM}_1\), zie wederom figuur 1. Een monetair gefinancierde verhoging van de overheidsuitgaven leidt daarom altijd tot een stijging van het inkomen (van \(Y_0\) naar \(Y_2\)), maar heeft een ambigu effect op de rente; \(i_2\) kan namelijk zowel boven als onder \(i_0\) liggen.

Alleen als de stijging van de geldvraag kleiner is dan de toename van het geldaanbod daalt de rente. MMT claimt echter dat de rente altijd daalt na een monetair gefinancierde verhoging van de uitgaven. Dit is daarom niet zonder meer juist in het IS-LM-model. Figuur 1 toont het geval waarbij de rente nog altijd stijgt.

MMT’ers stellen ook dat verdringing van consumptie of investeringen niet optreedt bij een hogere rente (Kelton, 2020). Dit wordt in de context van het IS-LM-model meestal geïnterpreteerd als een verticale IS-curve (\(f = 0\)) (DeLong, 2019; Jayadev en Mason, 2018; Rowe, 2011; Wren-Lewis, 2016). In dat geval reageren consumptie noch investeringen op de rente. Of de IS-curve dalend of verticaal is, maakt echter niet uit voor het effect op de rente. Dat wordt alleen bepaald door het effect van monetair gefinancierde overheidsuitgaven op de geldvraag en het geldaanbod. De stelling dat de rente zal dalen na een monetair gefinancierde uitgavenverhoging omdat de bestedingen niet zouden reageren op de rente, is daarom onjuist in het IS-LM-model.

Belastingen om inflatie te voorkomen

MMT bepleit verhoging van de belastingen om stijgende inflatie te voorkomen als de overheid haar hogere uitgaven monetair financiert. Maar hoeveel moet de belasting dan toenemen, en wat gebeurt er vervolgens met het begrotingstekort?

Om inflatie te analyseren, kan het IS-LM-model worden uitgebreid met een Phillipscurve of een geaggregeerde aanbodcurve (Mankiw, 2019). Deze geeft het verband tussen het prijspeil \(P\), het potentiële inkomen \(Y^*\), en het prijspeil bij volledige bezetting \(P^*\) (als \(Y = Y^*\)):

\(Y = Y^* + α(P − P^*)\). (3)

\(α > 0\) is de coëfficiënt die de prijs- en loonflexibiliteit in de economie meet. Hoe lager \(α\), hoe flexibeler de economie.

Stel dat in de situatie voor de budgettaire expansie de economie met onderbesteding kampt en het inkomen onder het potentiële inkomen ligt (\(Y < Y^*\)). De overheid verhoogt haar uitgaven (\(dG > 0\)) en financiert deze monetair (\(dG = dM\)). Het doel van MMT is om te zorgen dat de outputgap zich uiteindelijk precies sluit (\(dY = Y^* − Y\)) om zodoende volledige bezetting en werkgelegenheid te realiseren. De prijzen zullen door deze inkomenstoename ook stijgen. Een prijsstijging bij onderbesteding is niet een probleem, zolang de prijzen lager blijven dan het prijspeil bij volledige bezetting (\(P < P^*\)). In MMT moet belastingverhoging voorkomen dat de begrotingsimpuls overbesteding veroorzaakt (\(Y > Y^*\)), en het prijspeil hoger wordt dan het prijspeil bij volledige bezetting (\(P > P^*\)). De geaggregeerde aanbodcurve impliceert dat de prijsstijging bij sluiting van de outputgap gelijk is aan (minus) de outputgap gedeeld door \(α\) (\(dP = P^* − P = (Y^* − Y)/α\)).

Samenvattend: beginnend vanuit een situatie met onderbesteding (een negatieve outputgap Y < Y^*), leidt een toename van de overheidsuitgaven (dG > 0) tot drie effecten op de macro- economie: ten eerste een toename van de bestedingen omdat de overheidsuitgaven toenemen; ten tweede een toename van de geldhoeveelheid omdat de hogere uitgaven monetair worden gefinancierd (dG = dM > 0); en ten derde een verandering van de belastingen (dT) zodanig dat de outputgap wordt gesloten (dY = Y^* − Y) en de prijzen op het langetermijnprijspeil komen te liggen (dP = (Y^* − Y)/α). Om het effect van al deze gelijktijdige beleidswijzigingen te kunnen begrijpen is een model nodig; er veranderen simultaan drie beleidsvariabelen en drie uitkomstvariabelen.

Figuur 2 toont grafisch wat er gebeurt als de belastingen moeten stijgen om overbesteding door hogere overheidsuitgaven die monetair worden gefinancierd te voorkomen. De uitgavenverhoging leidt tot een verschuiving van de IS-curve naar rechts van \(\textrm{IS}_0\) naar \(\textrm{IS}_1\) en de monetaire expansie leidt tot een verschuiving van de LM-curve naar rechts van \(\textrm{LM}_0\) naar \(\textrm{LM}_1\), net zoals in figuur 1. Door de stijging van het inkomen naar het potentiële inkomen stijgt het prijspeil van \(P\) naar \(P^*\). Dit zorgt voor een daling van het reële geldaanbod en een verschuiving van de LM-curve van \(\textrm{LM}_1\) naar \(\textrm{LM}_2\), hetgeen een drukkend effect heeft op het inkomen. Als de twee stimulansen van budgettaire en monetaire verruiming te sterk zijn, en het inkomen boven het potentiële inkomen terechtkomt, dan worden de belastingen verhoogd om te zorgen dat de economie wordt afgeremd zodat uiteindelijk het potentiële inkomen wordt bereikt zonder te hoge inflatie. De belastingverhoging leidt in dit geval tot een verschuiving van de IS-curve terug naar links, van \(\textrm{IS}_1\) naar \(\textrm{IS}_2\), waar het potentiële inkomen wordt bereikt (\(Y_2 = Y^*\)). Alle begrotingsstimulansen die zouden leiden tot oververhitting worden daarom (perfect) verdrongen door hogere belastingen.

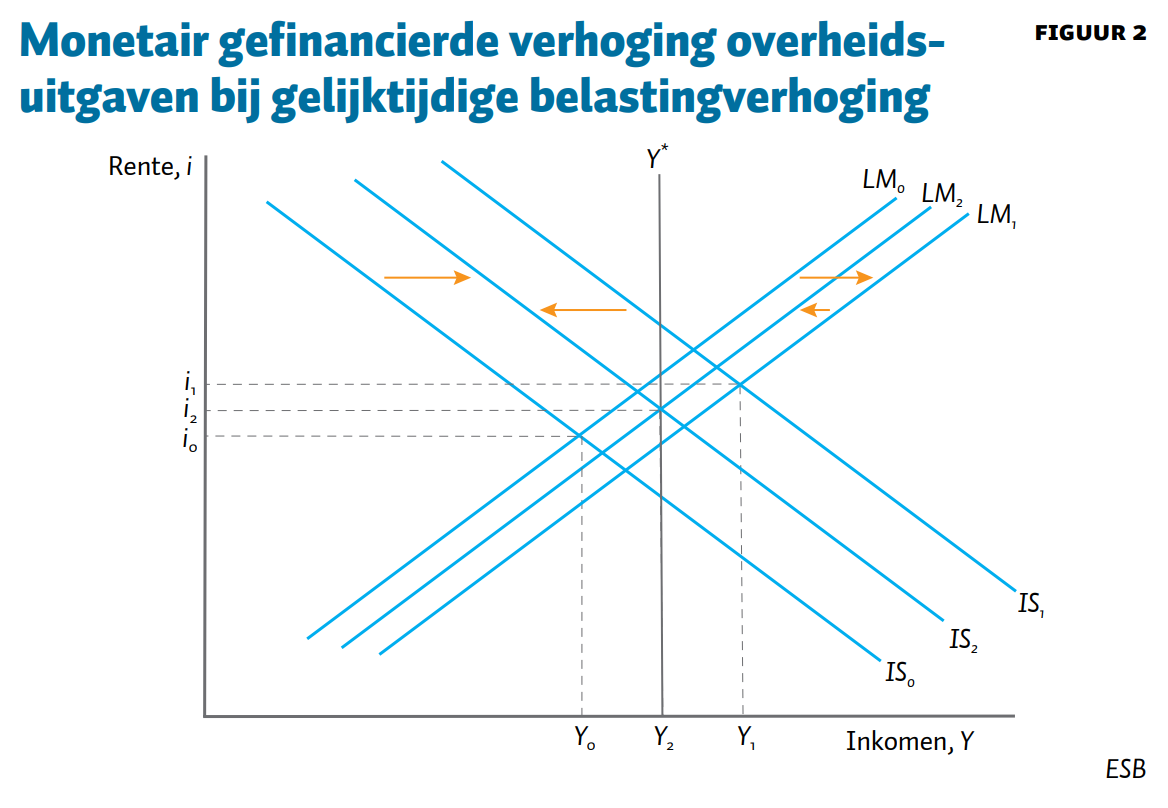
Ook hier kan de rente zowel stijgen als dalen: enerzijds leidt een monetaire expansie (\(dM > 0\)) tot een lagere rente. Anderzijds leiden het stimuleren van de economie (\(dY > 0\)) en de hogere prijzen (\(dP > 0\)) tot een hogere rente. Op voorhand is niet duidelijk welk effect sterker is. En ook hier hangt dit effect niet af van de rentegevoeligheid van de bestedingen (helling IS-curve).

De mate waarin de belastingen moeten stijgen om te zorgen dat de economie precies op het potentiële inkomen eindigt, is niet makkelijk te bepalen. Het hangt af van de mate van onderbesteding in de initiële situatie (\(Y^* − Y\)), de kracht van de bestedingsimpuls (\(dG\)) en de parameters van het IS-LM-model. Precieze uitspraken over het effect van een begrotingsimpuls op de hoogte van belastingen en het begrotingstekort zijn echter in twee speciale gevallen mogelijk.

Ten eerste, als er geen onderbesteding is (\(Y = Y^*\)) wanneer de monetair gefinancierde begrotingsimpuls wordt gegeven (\(dM = dG > 0\)). Het verhogen van de overheidsbestedingen in een conjunctureel neutrale situatie leidt altijd tot hogere belastingen en kleinere overheidstekorten. Door de begrotingsimpuls stijgt het inkomen via hogere bestedingen. De monetaire impuls doet dat ook: via een lagere rente nemen de bestedingen toe. Echter, als het inkomen zou gaan stijgen, dan wordt de outputgap positief (\(Y > Y^*\)) en stijgen de prijzen tot boven het structurele prijspeil (\(P > P^*\)).

Om dit te voorkomen verhoogt de overheid de belastingen. Het inkomen en de prijzen blijven vervolgens op het (structurele) niveau van de beginsituatie.

Ten tweede, als de rentegevoeligheid van de bestedingen nul is (\(f = 0\)). Dit lijkt vanuit MMT-perspectief een weinig controversiële aanname (Kelton, 2020; Mitchell et al., 2019; Wray, 2012). Het begrotingstekort blijft dan ongewijzigd (\(d(G − T) = 0\)) als de bestedingsimpuls van de overheid precies even groot is als de onderbesteding. De stijging van de belastingen is dan gelijk aan de stijging van de overheidsuitgaven (\(dT = dG\)). Zolang de overheid zorgt dat de onderbesteding precies verdwijnt, dan zal het begrotingstekort niet toenemen. Maar als de begrotingsimpuls groter is dan de onderbesteding, zoals in figuur 2 is aangenomen, dan moet volgens MMT het begrotingstekort wederom afnemen om stijgende inflatie te voorkomen.

Deze twee belangrijke speciale gevallen laten zien dat MMT geen theorie is van grotere begrotingstekorten, maar van kleinere begrotingstekorten. Alleen als de rentegevoeligheid van de bestedingen aanzienlijk zou zijn, dan kan een theoretische casus worden afgeleid waaronder de begrotingstekorten eventueel zouden kunnen toenemen. Maar deze casus lijken MMT’ers zelf weinig aannemelijk te vinden.

MMT gelijk aan Keynes

De economie bevindt zich al jaren in de keynesiaanse liquiditeitsval, waarin de ondergrens op de beleidsrente van de centrale bank is bereikt. Hoe verhouden de claims van MMT zich tot het IS-LM-model in de liquiditeitsval? Laat de effectieve ondergrens op de rente gelijk zijn aan \(i_\textrm{min}\). De LM-curve wordt dan horizontaal. Feitelijk wordt bij de ondergrens op de rente de interestgevoeligheid van de geldvraag oneindig groot (\(h = \infty\)). Figuur 3 toont deze situatie grafisch. Net als in figuren 1 en 2 neemt de vraag toe door de hogere overheidsuitgaven, waardoor de IS-curve verschuift van \(\textrm{IS}_0\) naar \(\textrm{IS}_1\). Maar bij een horizontale LM-curve treedt er geen verdringing meer op van de bestedingsimpuls. Het inkomen zal daarom met de multiplier \(m\) toenemen voor iedere euro waarmee de overheid haar bestedingen verhoogt. De rente zal niet veranderen en op de ondergrens blijven. De MMT-claim dat hogere overheidsuitgaven altijd leiden tot een lagere rente is bij de effectieve ondergrens triviaal onjuist, want deze kan niet verder dalen. Maar in de liquiditeitsval is de MMT-claim correct dat hogere tekorten niet tot verdringing leiden van de bestedingen via een hogere rente. Bovendien heeft MMT gelijk dat monetaire financiering bij de ondergrens geen probleem is. Het doet er bij de ondergrens namelijk niet toe of de begrotingsstimulans budgettair of monetair wordt gefinancierd. Bij een rente van nul zijn contanten en staatsobligaties perfect inwisselbaar geworden. De effecten op het inkomen en de rente zijn in beide gevallen identiek.

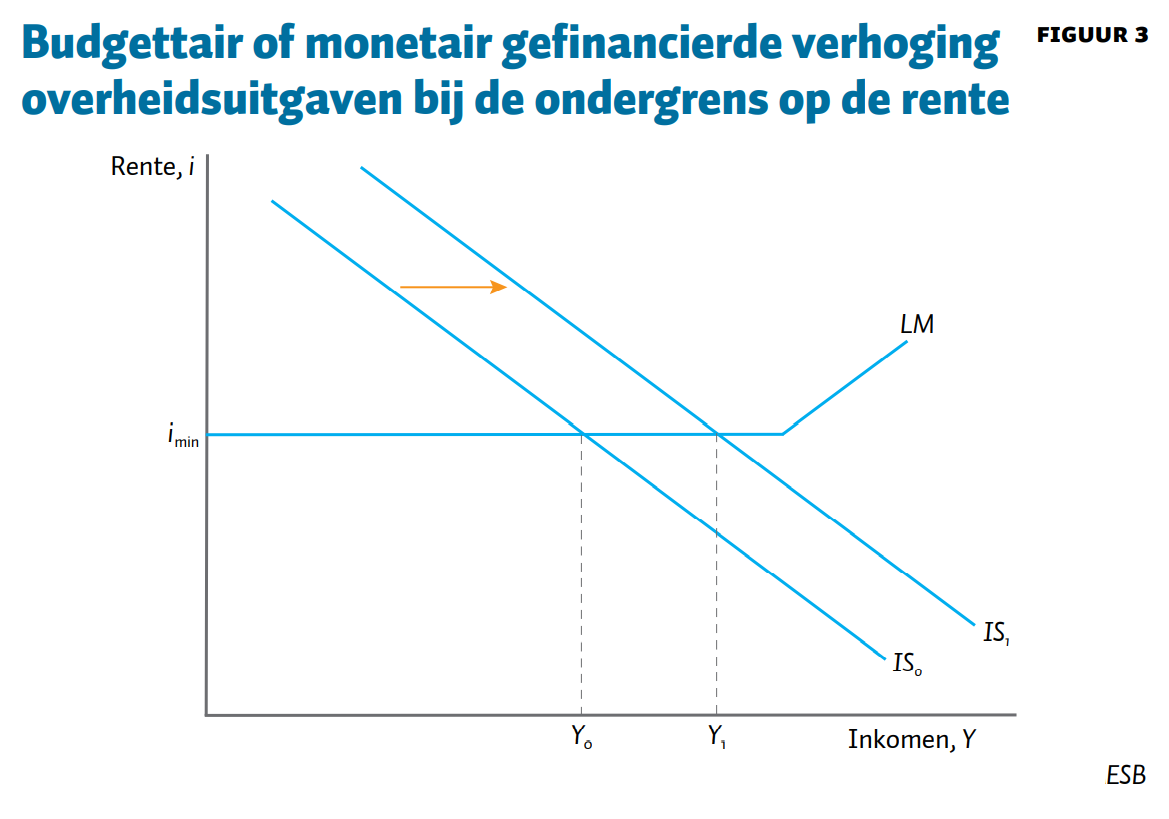
Ook bij de ondergrens op de rente kan het nodig zijn om de belastingen aan te passen bij een toename van de overheidsuitgaven, om te zorgen dat er overbesteding zou ontstaan en zo te voorkomen dat de inflatie zou oplopen, ongeacht of de overheidsuitgaven monetair of budgettair worden gefinancierd. De analyse van de belastingen en het begrotingstekort in de liquiditeitsval is analytisch identiek aan het tweede speciale geval waarin de rentegevoeligheid van de bestedingen nul is. Als de bestedingsimpuls van de overheid precies even groot is als de outputgap (\(dG = dY = (Y* − Y)\)), dan blijft het begrotingstekort ongewijzigd (\(d(G − T) = 0\)), en nemen de belastingen evenveel toe als de uitgaven (\(dT = dG\)). Wanneer de begrotingsimpuls echter leidt tot overbesteding (een positieve outputgap), dan moet het begrotingstekort kleiner worden. Dus ook bij de ondergrens op de rente is MMT een theorie van kleinere en niet van grotere overheidstekorten.

Discussie

Onder normale omstandigheden leiden monetair gefinancierde overheidsuitgaven niet altijd tot een lagere rente, zoals MMT’ers beweren. De rente zal alleen dalen als de geldvraag minder hard stijgt (vanwege de budgettaire expansie) dan het geldaanbod (vanwege de monetaire expansie), of als belastingverhogingen worden ingezet om oplopende inflatie te beteugelen. Bovendien wordt het effect op de rente niet bepaald door de rentegevoeligheid van de vraag (helling IS-curve), dus of er verdringing van overheidsbestedingen optreedt. MMT stelt hogere belastingen voor om te voorkomen dat de inflatie stijgt bij een monetair gefinancierde budgettaire expansie. Als monetair gefinancierde begrotingsimpulsen zorgen voor overbesteding, dan leidt dat typisch tot kleinere overheidstekorten wanneer belastingen toenemen om de inflatie te beteugelen.

In de liquiditeitsval, bij de ondergrens op de rente, is MMT en haar beleidsadvies nauwelijks te onderscheiden van de standaard keynesiaanse economie. Een standaardinzicht is dat het conventionele monetaire beleid niet meer kan worden gebruikt om de conjunctuur te stabiliseren, en dat het begrotingsbeleid dit dan moet doen. Ook een standaardinzicht is dat op de ondergrens begrotingsstimulansen niet tot meer inflatie leiden en dat monetaire financiering inwisselbaar is voor schuldfinanciering.

De analyse van MMT met het IS-LM-model, uitgebreid met een geaggregeerde aanbodcurve, leidt tot een aantal verrassende inzichten. Zouden die inzichten ook overeind blijven in meer gesofisticeerde modellen, zoals in gangbare nieuw-keynesiaanse modellen met een Taylor-regel voor het monetaire beleid (Woodford, 2003)? Alleen toekomstig onderzoek kan dat uitwijzen. Het is echter minder aannemelijk dat een vooruitkijkende geaggregeerde vraagcurve op basis van Calvo-prijszetting of een micro-gefundeerde IS-curve op basis van de Euler-vergelijking tot fundamenteel andere inzichten zullen leiden. De analyse van monetaire financiering wordt echter gecompliceerder. De centrale bank kan namelijk niet simultaan zowel de evenwichtsprijs (rente) als de evenwichts(geld)hoeveelheid op de geldmarkt bepalen, zoals MMT’ers lijken te suggereren (Kelton, 2020).

Tot slot, op de lange termijn, als lonen en prijzen volledig flexibel zijn, is geld neutraal en kan zowel budgettair als monetair beleid het inkomensniveau niet permanent verhogen. Het inkomen wordt op lange termijn vooral bepaald door het aanbod in de economie. Monetaire financiering kan dan geen substantiële bijdrage leveren aan de financiering van de overheid. MMT wekt echter sterk de suggestie dat geld op de lange termijn niet neutraal is, en het blijft onduidelijk waarom haar aanhangers dat vinden.

MMT maakt allerlei claims die of niet duidelijk of niet nieuw zijn. Het standaard IS-LM-model in de liquiditeitsval geeft al een jaar of tachtig, sinds Keynes (1936), dezelfde inzichten. MMT sticht vooral verwarring met het omdraaien van de rollen van monetair en budgettair beleid. Monetair beleid wordt ingezet voor de financiering van de overheid en budgettair beleid om de conjunctuur te stabiliseren. In tegenstelling tot pleidooien van MMT’ers voor veel grotere begrotingstekorten, is MMT paradoxaal genoeg vooral een theorie van de kleinere begrotingstekorten.

Literatuur

DeLong, B. (2019) Why people hate MMT? Grasping Reality, blog, 27 maart. Te vinden op www.bradford-delong.com.

Hicks, J.R. (1937) Mr. Keynes and the ‘classics’: a suggested interpretation. Econometrica, 5(2), 147–159.

Jayadev, A. en J.W. Mason (2018) Mainstream macroeconomics and Modern Monetary Theory: what really divides them? John Jay College, Department of Economics Working Paper, 2018-8. Te vinden op newserver.jjay.cuny.edu.

Kelton, S. (2019) Paul Krugman asked me about Modern Monetary Theory. Here are 4 answers. Te vinden op stephaniekelton.com.

Kelton, S. (2020) The deficit myth. Londen: John Murray.

Keynes, J.M. (1936) The general theory of employment, interest and money. Londen: Macmillan.

Lerner, A.P. (1943) Functional finance and the federal debt. Social Research, 10(1), 38–51.

Mankiw, N.G. (2019) Macroeconomics. Tiende editie. New York: MacMillan.

Mankiw, N.G. (2020) A skeptic’s guide to Modern Monetary Theory. The American Economic Review – Papers and Proceedings, 110, 141–144.

Mitchell, W., L.R. Wray en M. Watts (2019) Macroeconomics. Londen: Red Globe Press.

Rowe, N. (2011) Reverse-engineering the MMT model. Worthwhile Canadian Initiative, blog, 15 april.

Woodford, M. (2003) Interest and prices. Princeton: Princeton University Press.

Wray, L.R. (2012) Modern Monetary Theory: a primer on macroeconomics for sovereign monetary systems. Londen: Palgrave MacMillan.

Wray, L.R. (2021) Diverse blogs op neweconomicperspectives.org.

Wren-Lewis, S. (2016) MMT and mainstream macro. Blog op mainlymacro.blogspot.com, 22 maart.