Ik heb het uit. Thomas Piketty heeft met zijn Capital in the Twenty-First Century een fascinerend boek geschreven. Een boek dat mij dagen- en nachtenlang van de straat heeft gehouden en waarvan ik in de ban ben geraakt. Koop dat boek! Lees dat boek!
Piketty heeft echter wel onnodige verwarring bij mij gezaaid door de wijze waarop hij zijn race tussen arbeid en kapitaal presenteert. Piketty benadrukt dat deze race wordt verloren door arbeid doordat de groeivoet g van de economie daalt vanwege lagere bevolkingsgroei (vergrijzing) en tragere technische ontwikkeling en het rendement op kapitaal r gelijk blijft. Dus wordt r – g groter.
Piketty leidt dit af uit zijn twee ‘wetten’. De eerste ‘wet’ is een identiteit: het kapitaalaandeel in het bbp α = rβ is gelijk aan het rendement op kapitaal r maal de kapitaal-outputverhouding β = K/Y. De tweede ‘wet’ is een stationaire toestandsvergelijking: de kapitaal-outputverhouding wordt op lange termijn gelijk aan β = s/g waar s de spaarquote is van de economie. In de stationaire toestand van de economie wordt het kapitaalaandeel gelijk aan α = rs/g. Hieruit concludeert Piketty dat als de spaarquote s constant blijft, het aandeel van kapitaal α toeneemt als r – g groter wordt – mits de substitutie-elasticiteit tussen arbeid en kapitaal groter is dan 1. Daarover later meer.
Het probleem dat ik heb met deze voorstellig van zaken is dat de rentevoet r en de spaarquote s allebei endogeen zijn en niet zonder meer kunnen worden bepaald door extrapolatie van historische reeksen. Zie ook mijn eerste blog. Mijn belangrijkste kritiekpunt is dat Piketty geen enkele theorie over het spaargedrag formuleert waaruit zou moeten volgen dat r – g inderdaad groter wordt.
Echter, de these van Piketty houdt, zo blijkt, stand in alle standaard exogene groeitheorieën. Het is uiteindelijk heel simpel. Om Johan Cruijff te citeren: je gaat het pas zien als je het doorhebt. Maar voordat ik het doorhad moest ik het het vraagstuk van Piketty anders zien dan hij zijn lezers voorschotelt. Zijn hoofdresultaat volgt in minder dan een halve pagina.
Veronderstel dat de productie wordt beschreven door een productiefunctie Y = F(K, AL), waar Y staat voor het bbp, K voor kapitaal, A voor de productiviteit van arbeid en L voor arbeid. De functie F(.) heeft constante schaalvoordelen en afnemende meeropbrengsten naar kapitaal K en effectieve arbeid AL. Aangenomen wordt dat de substitutie-elasticiteit σ tussen kapitaal K en effectieve arbeid AL constant is (CES productiefunctie). In ‘intensieve vorm’ kunnen we de productiefunctie vervolgens schrijven als y = f(k) = [ωkϕ+(1-ω)]1/ϕ, ϕ ≡ (σ-1)/σ, waar y = Y/(AL) en k = K/(AL) staan voor het inkomen en kapitaal per ‘effectieve’ werknemer. De bevolking groeit met een constant percentage, dL/L = n, net als de techniek, dA/A = x. In de stationaire toestand van de economie – de aanname die Piketty maakt – wordt de kapitaal-arbeidverhouding k constant. Kapitaal K en de productie Y groeien ook met de groeivoet g = n + x. Op een concurrerende kapitaalmarkt is het rendement op kapitaal gelijk aan r = f’(k). Het aandeel van kapitaal in het bbp kan vervolgens worden geschreven als: α = f’(k)k/f(k). De centrale these van Piketty is dat α toeneemt als g = n + x daalt. Het enige dat we moeten weten is of ∂α/∂g = (∂α/∂k)×(∂k/∂g) > 0. Merk op dat α = f′(k)k/f(k) = ωkϕ/(ωkϕ+(1 – ω)), differentiëren geeft ∂α/∂k = ϕω(1 – ω)kϕ-1/(ωkϕ+ 1 – ω)² ≷ 0 ⇔ σ ≷ 1. Dus als de substitutie-elasticiteit σ tussen arbeid en kapitaal groter (kleiner) is dan 1, dan weten we dat ∂α/∂k > 0 (∂α/∂k < 0). Het laatste dat we dan nog moeten weten is of de kapitaal-arbeidverhouding k toe- of afneemt in de stationaire toestand van de economie. Uit alle standaard groeitheorieën (Ramsey, 1928; Solow, 1956; Samuelson, 1958) weten we dat k stijgt als de groei g daalt door een lagere bevolkingsgroei n of minder technische ontwikkeling x. De reden is dat arbeid relatief schaarser wordt ten opzichte van kapitaal bij een lagere groeivoet van de effectieve beroepsbevolking. Dus geldt dat ∂k/∂g < 0. We vinden dan inderdaad dat het kapitaalaandeel α stijgt als de groei g daalt: ∂α/∂g < 0. QED.
We hebben dus niet de ‘wetten’ nodig van Piketty om te begrijpen wat er zal gebeuren. We hoeven ook niet te kijken naar wat er met r gebeurt. Nota bene, het rendement op kapitaal daalt – en blijft niet constant zoals Piketty suggereert – want ∂r/∂k = f’’(k) < 0. Dat is logisch: als kapitaal overvloediger wordt ten opzichte van arbeid, daalt het rendement op kapitaal. Echter, als de substitutie-elasticiteit σ kleiner is dan 1, dan neemt het rendement op kapitaal r minder snel af dan de groeivoet g van de economie. Dus is een toename van het inkomensaandeel van kapitaal α equivalent aan een toename van het verschil van r – g. De antwoorden op volgende twee vragen zijn daarom kritiek of Piketty’s voorspelde terugkeer naar de klassensamenleving zal plaatsvinden.
1. Neemt de kapitaal-arbeidverhouding op lange termijn toe? Dat is theoretisch en empirisch aannemelijk, omdat de bevolking vergrijst en de technologische verandering daalt. De ultieme vraag is niet of de kapitaal-outputverhouding zal gaan stijgen. Daar ben ik het met Piketty eens; die stijgt zeer waarschijnlijk gewoon door. De vraag is alleen met hoeveel. In mijn vorige blog heb ik laten zien dat de conclusies van Piketty extreem gevoelig zijn voor de aannames van het spaargedrag. Voor het echte antwoord hebben we een empirisch en theoretisch solide onderbouwde spaartheorie nodig. En die ontbreekt helaas in Piketty’s boek.
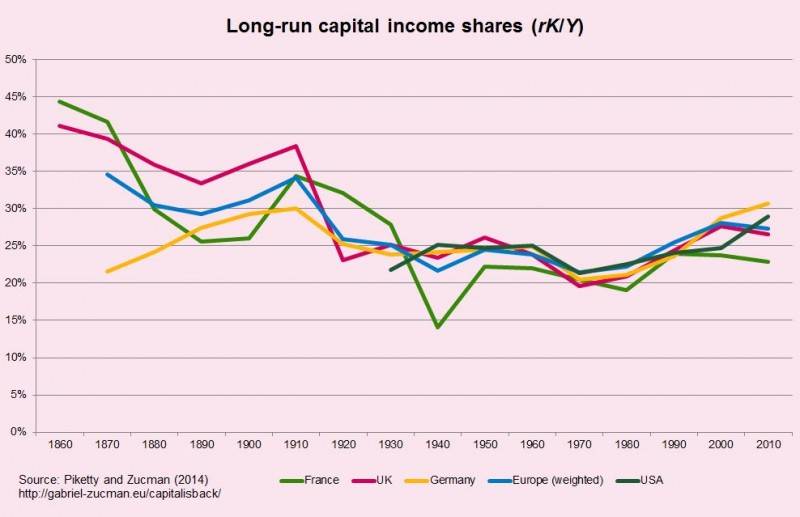
2. Is de substitutie-elasticiteit tussen arbeid en kapitaal σ wel groter 1? Hoe hoger (lager) σ hoe makkelijker (moeilijker) arbeid kan worden vervangen door kapitaal. Als kapitaal sterk groeit dan bepaalt σ hoe sterk het rendement r zakt. Als σ > 1, dan daalt weliswaar het rendement op kapitaalinkomen (prijseffect), maar als werknemers makkelijk kunnen worden vervangen door kapitaal, dan is dat prijseffect beperkt. De groei van kapitaal (volume-effect) is dan groot genoeg om de dalende rendementen (prijseffect) te compenseren zodat dat het kapitaalaandeel in het bbp toch stijgt. Hier wijkt Piketty feitelijk af van Karl Marx. Heel vrij geïnterpreteerd (ben geen Marx-expert): Marx dacht dat σ < 1. De ‘winstvoet’ (prijseffect) daalde zo sterk dat het kapitaalaandeel daalde ondanks sterkere kapitaalaccumulatie (volume-effect). Empirisch worden meestal schattingen kleiner dan 1 gevonden voor de substititutie-elasticiteit, zie bijvoorbeeld Chirinko (2002). Echter, ik ben het met Piketty eens dat we dan niet goed begrijpen hoe kapitaalrendementen en kapitaalaandelen door de tijd veranderen. Als σ < 1 dan zouden we moeten zien dat het kapitaalaandeel in het bbp structureel zou moeten dalen als de kapitaal-bbp verhouding sterk stijgt. En hoewel dat laatste wel is gebeurd, hebben we sinds de jaren 80 niet meer een gestage daling van het kapitaal-bbp aandeel waargenomen. Zie ook de figuur. Het kan zijn dat σ rond 1980 is omgeklapt van een getal kleiner naar een getal groter dan 1.
Conclusie
Het is waarschijnlijk dat kapitaal nog belangrijker wordt dan het al is. Maar of de voorspelling van Piketty uitkomt, dat we terugkeren naar de rentenierssamenleving, is lang niet zeker, zoals ik eerder heb betoogd. De hamvraag is hoeveel mensen bereid zijn te gaan sparen – als de samenleving vergrijst en er minder technologische vooruitgang is – en dus hoe groot de steady-state kapitaal-arbeidverhouding wordt op lange termijn. Op die vraag geeft het boek van Piketty helaas niet het finale antwoord. De tijd zal het leren.
Auteur
Categorieën