Nederlandse ziekenhuizen te groot voor verdere schaalvoordelen

• VanHulst Blank (2017) ESB 4749 226-228.pdf Download [176,45 kb]

Door fusies zijn Nederlandse ziekenhuizen in de laatste decennia steeds groter geworden. Uit een meta-analyse van internationale studies blijkt dat de zorgkosten juist het laagst zijn in ziekenhuizen die kleiner zijn dan de meeste Nederlandse ziekenhuizen. Het is daarom onwaarschijnlijk dat verdere schaalvergroting de zorg­kosten zal drukken.

In de Nederlandse ziekenhuissector is er al ­jaren sprake van een proces van schaalvergroting. De afgelopen dertig jaar is het aantal algemene zieken­huizen gehalveerd, voornamelijk als gevolg van ­fusies (Blank, 2015). De laatste jaren is er wederom sprake van een fusiekoorts. In een eerdere ESB is al aangetoond dat ziekenhuisfusies niet aantoonbaar ­leiden tot ­betere kwaliteit (Batterink et al., 2017). Ook de ­mogelijk ­beoogde kostenbesparingen van een verdere conso­lidatieslag zijn twijfelachtig. De gemiddelde kostencurve heeft namelijk een U-vormig verloop: eerst gaat schaalvergroting gepaard met dalende gemiddelde kosten, vervolgens is er een omslagpunt waarna de kosten sneller toenemen dan de productie. Nederlandse ziekenhuizen zijn al voorbij dit omslagpunt. Blank en Van Hulst (2013) constateren dat een gemiddeld Nederlandse ziekenhuis juist te maken heeft met schaal­nadelen.

Het is echter niet duidelijk wat de optimale schaal voor een zieken­huis dan wel is, mede omdat de schaal in ­Nederland zover is doorgeschoten dat de optimale schaal niet meer empirisch kan worden vastgesteld. Eerdere ­studies naar de kostenstructuur van ­Nederlandse ziekenhuizen geven ook geen uitsluitsel over de optimale schaal, en presenteren alleen schaaleffecten voor een gemiddeld ziekenhuis (Blank en Eggink, 2004; Blank en Merkies, 2004; Blank en Vogelaar, 2004; Blank en Van Hulst, 2009; Ludwig et al., 2009; 2010). Inzicht in de optimale schaal ontbreekt dus. Door deze studies door de tijd heen te verge­lijken, kan worden geconcludeerd dat voor ziekenhuizen als gevolg van schaalvergroting de schaalvoordelen zijn ­afgenomen en zijn omgeslagen in schaalnadelen. Mogelijk kan een meta-analyse van de internationale literatuur ­inzicht bieden in de ­optimale schaal van ziekenhuizen, omdat met een verscheidenheid aan resultaten een omslagpunt bepaald kan worden.

Schaalelasticiteit en ziekenhuisomvang

Omdat studies naar de kostenstructuur van ziekenhuizen niet direct de optimale omvang rapporteren, moet deze indirect worden afgeleid uit datgene wat studies wel rapporteren: een combinatie van de schaalelasticiteit en de omvang van het ziekenhuis. Een schaalelasticiteit geeft aan met hoeveel procent de productie toeneemt bij een toename van de kosten met één procent. Bij een schaalelasticiteit van één is de schaal optimaal, terwijl er sprake is van schaalvoordelen en schaalnadelen als de schaalelasticiteit groter respectievelijk kleiner is dan één. De kosten groeien dan immers langzamer respectievelijk sneller dan productie. De schaalelasticiteit hoeft niet overal gelijk te zijn en kan variëren met de omvang van het ziekenhuis.

In vergelijking met andere indicatoren voor schaal­omvang – zoals productie, opnamen, omzet en kosten – is het aantal bedden de meest praktische indicator voor de schaal van een ziekenhuis. Het aantal bedden wordt in ­bijna alle studies vermeld en is, onder andere vanwege ­geringe ­definitieverschillen, goed te vergelijken tussen de ­verschillende studies. Een nadeel is dat het aantal bedden een grove indicator is voor de omvang van de productie.

Data en methode

De benodigde data over omvang en schaalelasticiteit zijn gevonden door in de databases van Web of Science en PubMed te zoeken naar empirische ­studies ­inzake de kosten­structuur of productiestructuur van zieken­huizen. De gevonden literatuur is verder uitgebreid door te zoeken in Google Scholar en door het opnemen van kruisverwijzingen uit de gevonden literatuur. Daarbij is geselecteerd op studies van na 1990, die bovendien ­betrekking hebben op westerse landen. Ook zijn de studies beoordeeld op basis van een aantal praktische criteria, zoals de rapportage van de schaalelasticiteit bij een bepaalde omvang of de mogelijkheid om deze eruit af te leiden.

Deze zoekmethode heeft 41 bruikbare studies en 95 waarnemingen van de schaalelasticiteit opgeleverd. Er zijn drie redenen waarom sommige studies meerdere schaal­elasticiteiten presenteren. Ten eerste rapporteren studies, behalve resultaten wat betreft het gemiddelde, soms ook ­resultaten voor het eerste en derde kwartiel. Ten tweede zijn er studies die rapporteren aangaande diverse sub-­samples, bijvoorbeeld aparte samples voor ziekenhuizen met en zonder winstuitkering. Ten slotte zijn er studies die resultaten geven voor verschillende specificaties van de kostenfunctie.

Studiekenmerken

Naast de omvang van het ziekenhuis zijn ook studiekenmerken van invloed op de gevonden schaalelasticiteit. Zo impliceert de specificatie van de kostenfunctie in iedere studie een veronderstelling over de kostenstructuur; een Cobb-Douglas-kostenfunctie impliceert bijvoorbeeld dat de schaalelasticiteit bij elke omvang gelijk is. Een ander voorbeeld is de wijze waarop de schaalelasticiteit wordt ­afgeleid. Zo laten Braeutigam en Daughety (1983) zien dat het afleiden van de schaalelasticiteit uit de korte­termijn-kostenfunctie andere resultaten oplevert dan het gebruik van de langetermijn-kostenfunctie.

Bij het relateren van de schaalelasticiteit aan de ­omvang van een ziekenhuis is het daarom wenselijk om te controleren voor deze studiekenmerken (Van Hulst, 2016). Systematisch is een aantal studiekenmerken geïnventariseerd (tabel 1), zoals gebruik van een langetermijnkostenfunctie, gebruik van een frontier-functie, functionele vorm van de kostenfunctie, aantal gemodelleerde inputs en outputs, wijze waarop rekening wordt gehouden met casemix-verschillen, correctie voor omgevingskenmerken, studies uitgevoerd voor ziekenhuizen in de Verenigde ­Staten, en het aantal waarnemingen waarop het resultaat is gebaseerd.

Beschrijvende statistiek

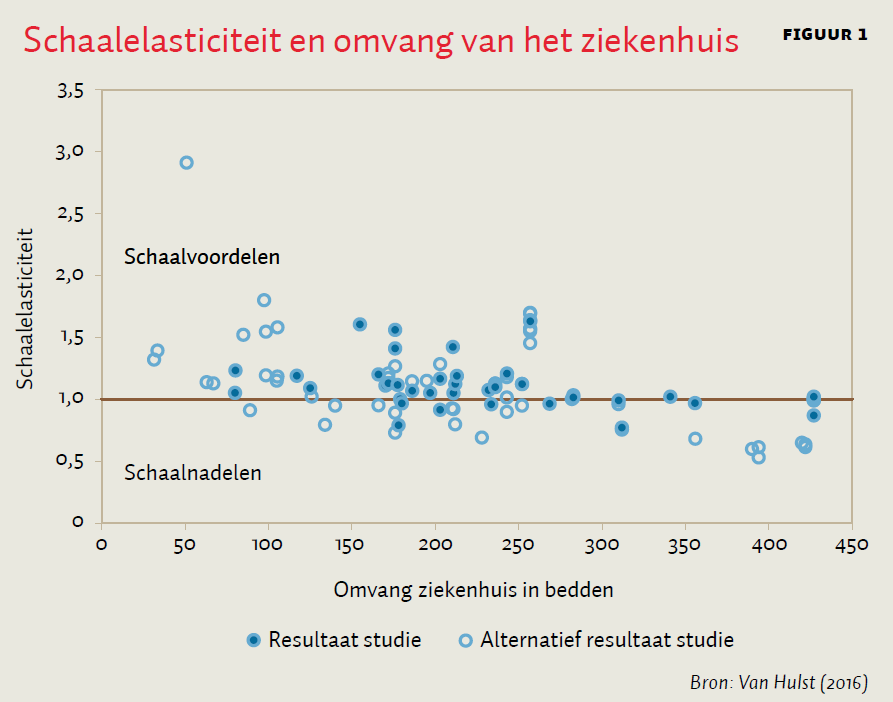
Als de schaalelasticiteit uit de gevonden studies tegen de omvang van het ziekenhuis wordt afgezet, blijkt grofweg dat de studies voor ziekenhuizen met minder dan 150 bedden voornamelijk schaalvoordelen vinden (figuur 1). Vanaf 150 bedden worden er wisselende resultaten gevonden, en naarmate de omvang van een ziekenhuis toeneemt, worden de resultaten met schaalvoordelen schaarser. Voorbij een omvang van 300 bedden worden er geen schaalvoordelen meer gevonden. De gemiddelde schaalelasticiteit van de 41 studies is 1,1 bij een gemiddeld aantal bedden van 240. ­Gemiddeld genomen vinden de studies schaalvoordelen, maar tegelijkertijd is de gemiddelde omvang van de ziekenhuizen aanzienlijk kleiner dan de gemiddelde omvang van een Nederlands ziekenhuis (met gemiddeld 450 bedden).

Optimale omvang

Om de optimale omvang van ziekenhuizen te bepalen is de schaalelasticiteit geregresseerd op de schaal van het ziekenhuis en de kenmerken van de studies waarmee de schaal­elasticiteit is bepaald. De regressie is uitgevoerd op zowel het niveau van de studies (N = 41) als het niveau van de waarnemingen (N = 95). Het merendeel van de studiekenmerken is opgenomen als dummyvariabele. De enige variabelen die continu zijn, zijn het aantal bedden en de steekproefomvang. Mogelijk zijn de effecten voor deze ­variabelen niet lineair, maar nemen deze geleidelijk af. Daarom zijn ook specificaties geschat met de logaritme van die variabelen. Uit statistische toetsen blijkt dat voor het aantal bedden de lineaire specificatie de beste optie is, en voor de steekproefomvang heeft de logaritme de voorkeur. In meta-regressieanalyses is het gebruikelijk om de waarnemingen te wegen, om zodoende aan meer betrouwbare studies meer gewicht te geven. De in studies gevonden schaalelasticiteiten hebben immers een standaardfout, en een kleinere standaardfout impliceert een betrouwbaarder resultaat. Naast betrouwbaarheid is er ook een effect te verwachten als studies betrekking hebben op verschillende populaties. In deze studie is met beide effecten rekening ­gehouden door de random–effects-methode toe te passen (Van Hulst, 2016).

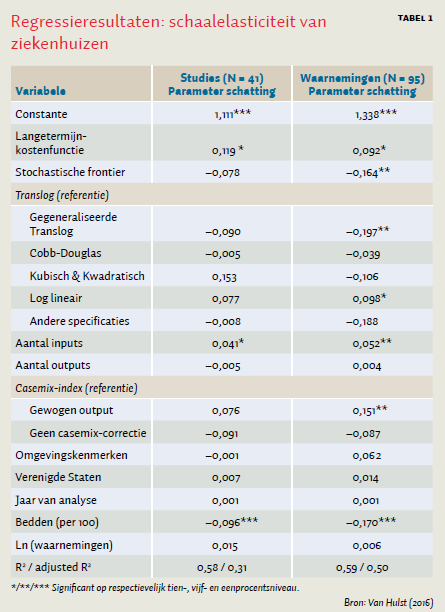
Het aantal bedden, een indicator voor de omvang van het ziekenhuis, is een significante en belangrijke determinant voor de schaalelasticiteit. Per honderd bedden neemt de schaalelasticiteit af met 0,1 (studies) tot 0,17 (waarnemingen). Met dit schattingsresultaat kan de optimale schaal van een ziekenhuis worden bepaald door voor een referentiestudie uit te rekenen bij welke schaal de schaal­elasticiteit gelijk is aan 1. De referentiestudie is gebaseerd op kenmerken die het meest worden gebruikt in studies. Deze studie is: short-run, geen frontier, translog, maakt gebruik van een casemix-index, en betreft niet de Verenigde Staten (Van Hulst, 2016). Voor de referentiestudie komt de optimale schaal uit op 320 bedden.

Uit geschatte parameters van de studiekenmerken valt ook af te leiden wat de effecten zijn van verschillende studie­kenmerken op de optimale schaal. Zo is de gebruikte referentiestudie geen stochastische frontier, dus als we dit kenmerk veranderen, dan wijzigt de optimale schaal. Voor een referentiestudie waarin we alleen dit kenmerk veranderen in stochastische frontier is het optimum 240 bedden. Het gebruikte type studie is dus van invloed op het resultaat. Juist voor de optimale schaal kan het punt worden ­gemaakt dat dit een frontier-eigenschap is.

De schattingsresultaten laten zien dat de verklarende variabelen een redelijk deel van de variatie van de schaalelasticiteit verklaren. Wel is bij de regressie op studies het aantal vrijheidsgraden beperkt, als gevolg hiervan is de ­gecorrigeerde R2 met een waarde van 0,31 aanzienlijk lager dan de ongecorrigeerde R2 van 0,58. Het effect van de vrijheidsgraden heeft vooral effect op de fit, bij minder verklarende variabelen blijven uitkomsten vergelijkbaar. Ook de schattingsresultaten op waarnemingen laten vergelijkbare resultaten zien.

Conclusie

Uit een meta-analyse van de internationale literatuur vinden we dat de optimale schaal voor ziekenhuizen ongeveer 320 bedden is. Dit resultaat is in de buurt van de bovengrens van Aletras (1997), die concludeert dat de meeste studies constante schaalopbrengsten of zelfs schaalnadelen vinden voor ziekenhuizen tussen de 200 en 300 bedden. Van schaalvergroting voorbij de 320 bedden is dus waarschijnlijk geen verdere daling van de gemiddelde kosten te verwachten. Daarbij is 320 bedden mogelijk een ruime bovengrens, omdat studies die gebruikmaken van een ­stochastische frontier een aanzienlijk lager omslagpunt van de gemiddelde kosten vinden.

De mogelijkheid tot het behalen van schaalvoordelen is vooral aanwezig bij kleine ziekenhuizen. Aangezien een gemiddeld Nederlandse ziekenhuis 450 bedden heeft en slechts een kwart van de Nederlandse ziekenhuizen minder dan 300 bedden heeft, lijkt het merendeel van de Nederlandse ziekenhuizen te groot om schaalvoordelen te halen uit een fusie.

Literatuur

Aletras, V. (1997) Concentration and choice in the provision of hospital services. Part II: The ­relationship between volume and the scope of activity and hospital costs. York: University of York.

Batterink, M., M. Pomp, R. Kemp et al. (2017) Ziekenhuisfusies leiden niet aantoonbaar tot betere kwaliteit. ESB, 102(4745), 20-22.

Blank, J. (2015) Illusies over fusies. Een kritische beschouwing over de schaalvergroting in de Neder­landse publieke sector 1985–2012. Publicatiereeks Overheid en Arbeid, 41. Den Haag: CAOP.

Blank, J.L.T. en E. Eggink (2004) The decomposition of cost efficiency: An empirical application of the shadow cost function model to Dutch general hospitals. Health Care Management Science, 7(2), 79–88.

Blank, J.L.T. en B.L. van Hulst (2009) Productive innovations in hospitals: An empirical ­research on the relation between technology and productivity in the Dutch hospital industry. Health Economics, 18(6), 665–679.

Blank, J.L.T. en B.L. van Hulst (2013) Opereren bij schaalnadelen. Tijdschrift voor Openbare Financiën, 45(2), 75–81.

Blank, J.L.T. en A. Merkies (2004) Empirical assessment of the economic behaviour of Dutch general hospitals. Health Economics, 13(3), 265–280.

Blank, J.L.T. en I. Vogelaar (2004) Specifying technical change: A research on the nature of technical change in Dutch hospital industry. The Quarterly Review of Economics and Finance, 44(3), 448–463.

Braeutigam, R.R. en A.F. Daughety (1983) On the estimation of returns to scale using variable cost functions. Economics Letters, 11(1–2), 25–31.

Hulst, B.L. van (2016) Enhancing hospital productivity. Proefschrift. Technische Universiteit Delft.

Ludwig, M., W. Groot en F. van Merode (2009) Hospital efficiency and transaction costs: A stochastic frontier approach. Social Science & Medicine, 69(1), 61–67.

Ludwig, M., Frits van Merode en W. Groot (2010) Principal agent relationships and the ­efficiency of hospitals. European Journal of Health Economics, 11(3), 291–304.